[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Wie bei allen numerischen Problemen muß gleich zu Beginn eine Reihe von Fragen geklärt werden:
Was soll berechnet werden? Welche Eigenschaften hat das vorliegende Problem? etc. In diese Phase fällt auch die Bereitstellung und Erarbeitung von Grundlagen für die Algorithmus- bzw Software-Auswahl.
Zuerst ist zu klären, ob ein lineares oder ein nichtlineares Problem vorliegt (siehe auch 6.5).
Um ein lineares Gleichungssystem mit vorhandenen Softwareprodukten lösen zu können, bringt man es meist in die Standardform Ax=b.
Definition: Lineares Gleichungssystem, Standardform: Ein System von m Gleichungen in n Unbekannten x1,....,xn der Form
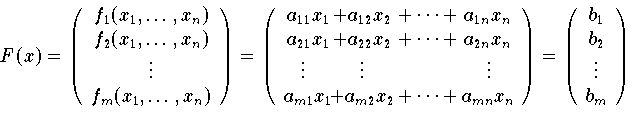
oder kürzer: Ax=b - in dem die Größen a11,...,amn
und b1,...,bm gegeben sind - nennt man ein lineares Gleichungssystem.
Dabei ist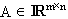 
die Koeffizientenmatrix (Systemmatrix),
der Vektor 
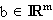die rechte Seite und 
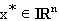ein
gesuchter Vektor, der simultan alle m Gleichungen erfüllt.
Folgende 3 Fälle sind bei linearen Gleichungssystemen hinsichtlich Auswahl geeigneter Lösungsverfahren zu unterscheiden:
m=n:
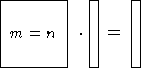
Es hängt von der Matrix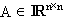 
ab, ob eine eindeutige
Lösung existiert. Wenn dies nicht der Fall ist, so existiert
je nach Konstellation der rechten Seite b entweder keine Lösung
oder ein ganzer Lösungsraum.
m<n:
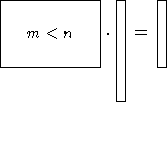
Anzahl der Unbekannten größer als die Anzahl
der Gleichungen. Ax=b ist ein unterbestimmtes lineares
Gleichungssystem. Derartige Systeme besitzen immer einen ganzen
Unterraum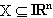 
mit einer Dimension dim(X)>=n-m als Lösung.
m>n:
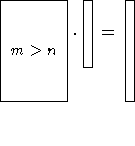
Mehr Gleichungen wie Unbekannte vorhanden. Ax=b ist ein überbestimmtes lineares Gleichungssystem, das in den meisten Fällen keine Lösung besitzt
Wenn gilt b=0 (homogen), dann sind andere Lösungswege erforderlich (siehe auch 8.7.5)
Liegen mehrere lineare Probleme
Ax1=b1, Ax2=b2,...,Axk=bk
mit verschiedenen rechten Seiten, aber einer gemeinsamen Matrix A vor, so entspricht die gemeinsame Lösung der k Gleichungen der Lösung einer einzigen Matrixgleichung
AX=B, ,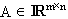 
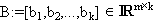
Liegen nicht alle Daten der Gleichungen gleichzeitig vor, so können diese auch nicht gemeinsam als eine Matrixgleichung gelöst werden. In diesem Fall ist ein mehrstufiger Lösungsvorgang angebracht: Zuerst wird die Matrix A mit einem O(n3)-Aufwand faktorisiert. Mit den Faktormatrizen wird dann sukzessive eine Gleichung nach der anderen mit O(n2) Gleitpunktoperationen gelöst.
der Koeffizienten ist ein wichtiges Merkmal des Problemtyps. Gleitpunkt-Datentypen wie REAL, COMPLEX etc. spielen vor allem bei der Wahl der Software eine wichtige Rolle.
Bei der Suche nach einer ganzzahligen Lösung handelt es sich um einen völlig anderen Problemtyp.
Eine wichtige Klassifizierung des Problemtyps erfolgt durch Art und Größe der Datenfehler. Bei den meisten überbestimmten Systemen sind die Komponenten des Vektors b und oft auch die Koeffizienten a11,...,amn mit Ungenauigkeiten behaftet. In solchen Fällen sollten schon während der Planungsphase Konditionsuntersuchungen vorbereitet werden. Hier empfiehlt sich eine Lösung durch orthogonale Approximation.
Die Ermittlung einer Lösung fehlerbehafteter überbestimmter Systeme nach der Methode der kleinsten Quadrate ist eigentlich nur für jene Probleme gedacht, bei denen b mit größeren Datenfehlern behaftet ist, die Koeffizienten a11,...,amn hingegen nur mit Störungen in der Größenordnung elementarer Rundungsfehler.
Die Eigenschaft der Symmetrie:
aij=aji für alle i,j e {1,2,....,n}
einer quadratischen Matrix 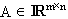ist leicht zu erkennen. Bei
ihnen läßt sich durch passende Speichertechniken der
Speicherbedarf nahezu halbieren. Mit spezieller Software kann auch der Rechenaufwand halbiert werden.
Im Gegensatz dazu ist die (positive) Definitheit:
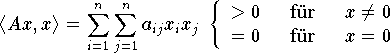
nicht so leicht zu erkennen. (siehe auch 8.5.3)
Bei sehr großen Systemen mit Tausenden bis Hunderttausenden Gleichungen spielt der Besetztheitsgrad der Matrix mit Nichtnullelementen eine fundamentale Rolle:
Schwach besetzte Matrizen sind Matrizen für die gilt:
sehr viele Elemente aij=0
solche Gleichungssysteme können mit geeigneter Software selbst bei einer Dimension n=100000 gelöst werden. Bei einer vollbesetzten Matrix dieser Größenordnung ist das Problem selbst auf einem modernen Supercomputer praktisch unlösbar.
Bei einer schwach besetzten Matrix ist auch die Besetztheitsstruktur von Bedeutung für Algorithmus- und Softwareauswahl. Dabei spielen die Bandmatrizen eine wichtige Rolle, weil es für sie spezielle, sehr effiziente Algorithmen gibt.
Lineare Gleichungssysteme sind besonders "angenehme" numerische Probleme:
1. Daten zur Spezifikation liegen von Haus aus als algebraische Daten vor.
2. Zur algorithmischen Lösung ist keine Finitisierung erforderlich.
Schwierigkeiten bereiten jene Probleme, bei denen die Systemmatrix A nicht regulär ist. Dies umso mehr, als im Fall schlecht konditionierter Probleme die im mathematisch-analytischen Sinn völlig klare Fallunterscheidung
A ist regulär oder A ist singulär
durch Daten- und Rechenfehler zu einer unscharfen Entscheidung zwischen numerisch regulär und numerisch singulär wird, die sich überhaupt nur unter Berücksichtigung zusätzlicher Informationen (z.B. über Art und Größe der Datenfehler) sinnvoll treffen läßt.
Eine mögliche Lösungsdefinition im numerisch singulären Fall ist die Pseudo-Normallösung
x0=A+b
die mit Hilfe der verallgemeinerten Inversen A+ definiert ist. Für die praktische Ermittlung von A+ ist die sogenannte Singulärwertzerlegung ein wichtiges Hilfsmittel.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ] Jürgen Tschirnich