[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Badr Baher 9126201 881
Im Abschnitt 8.4.5 wurde die Verbindung hergestellt zwischen den linearen Abbildung (Funktionen)
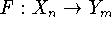
Ym und den Matrizen als Koordinaten der Bilder von Basisvektoren
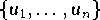
des Xn . Alle Matrizen, die eine gegebene lineare Abbildung hinsichtlich irgendwelcher Basen darstellen, kann man in einer Äquivalenzklasse zusammen fassen.
Äquivalenz von Matrizen: zwei mn-Matrizen A und B sind Äquivalent, wenn es reguläre Matrizen R und T mit B=RAT gibt.Wenn es zwei Orthogonale Matrizen U und V mit B=UT AV gibt, so nennt man A und B orthogonal-äquivalent.
Singulärvektoren: Die Matrix U besteht aus den orthonormierten Eigenvektoren u1,...,um von AAT , die man Linkssingulärvektoren von A nennt, und die Matrix V aus den orthonormierten Eigenvektoren v1,...,vn von AT A, den Rechtssingulärvektoren von A.
Singulärwerte:
Die Diagonalelemente 1,...,k der zu A orthogonal-äquivalenten Diagonalmatrix S nennt die Singulärwerte der Matrix A.
Aus der Singulärwertzerlegung
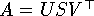
läßt sich sehr viel über die Struktur der von einer Matrix ARnn dargestellt linearen Abbildung unmittelbar ablesen. So erhält.
Verbindungsraum, direkte Summe:
Für zwei Unterräume S1 und S2 des Rn bezeichnet man den Unterraum
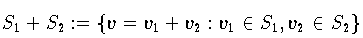
als Verbindungsraum; wenn zusätzlich S1 S2={0} gilt, so bezeichnet man den Verbindungsraum
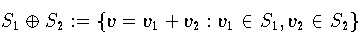 als direkte Summe von S1 und S2 .
als direkte Summe von S1 und S2 .
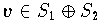
kann eindeutig in der Form
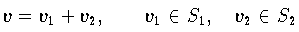
zerlegt werden. Der Vektor vi heißt die orthogonale Projektion von v auf den Unterraum
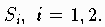 .
.
Für eine lineare Abbildung A: U W gilt:
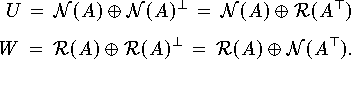 .
.
Alle Vektoren uU und wW können daher durch
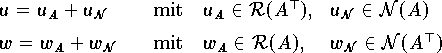 .
.
in eindeutiger Weise in orthogonale Komponenten (siehe Abbildung) zerlegt werden. uA ist die orthogonale Projektion von u auf
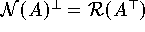 .
.
Die entsprechende Projektionsabbildung wird mit
 .
.
bezeichnet. Analog stellt
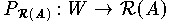
die Projektion auf den Bildraum von A dar.
Jede Abbildung A läßt sich als zusammengesetzte Abbildung
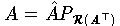 darstellen, wobei
darstellen, wobei 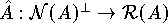 die Einschränkung
von A auf
die Einschränkung
von A auf 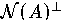 ist:
ist:

Die Abbildung 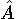 ist Injektiv und besitzt daher eine Inverse
ist Injektiv und besitzt daher eine Inverse
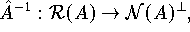
mit deren Hilfe man eine neue Abbildung definieren kann, die zu einer Verallgemeinerung der Inversen einer Matrix führt.
Verallgemeinerte Inverse, Pseudo-Inverse :Durch
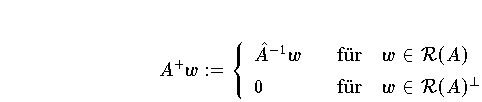
wird die zusammengesetzte Abbildung

festgelegt, die man verallgemeinerte Inverse oder Pseudo-Inverse A+ von A nennt.
Die so definierte Pseudo-Inverse ist eindeutig bestimmt und erfüllt die folgenden vier Beziehungen:
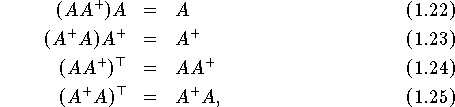
die sogenannten Moore-Penrose-Bedingungen. Aus (13,22) und (8.24) folgt
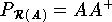
und aus (8.23) und (8.25)
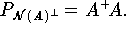 .
.
Ist ARnn regulär, so sind die Projektionen
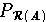 und
und 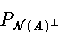
identische Abbildungen und es gilt
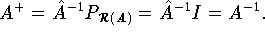
Mit Hilfe der verallgemeinerten Inversen kann man sämtliche Fälle, die bei der Lösung inhomogener linearer Gleichungssysteme Ax =b mit b#0 und ARnn auftreten können, in völlig einheitlicher Weise behandeln.
Reguläre Matrix
Ist ARnn eine reguläre Matrix, d.h. gilt rang(A)=n, so folgt aus A+= A-1 die Lösung
x0= A-1b
des Gleicchungssystems Ax =b. Die praktisch-algorithmische Ermittlung der Lösung, die man aus Effizienzgründen nicht mit Hilfe von A-1, sonders mit geeigneten Faktorisierungen von A vornimmt, wird in späteren Abschnitten behandelt; ebenso jene Fälle, wo A zwar regulär, aber schlecht konditioniert ist .
Singuläre Matrix
Ist ARnn eine singuläre Matrix mit rang(A)=k <n, so müssen zwei Fälle unterschieden werden.
Fall 1: 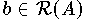
In diesem Fall ist der Vektor  Lösung des Gleichungssystems,
aber auch jeder Vektor
Lösung des Gleichungssystems,
aber auch jeder Vektor
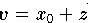 mit
mit
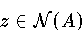
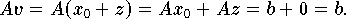 .
.
Das Gleichungssystem 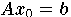 hat in diesem Fall die Lösungsmannigfaltigkeit
hat in diesem Fall die Lösungsmannigfaltigkeit
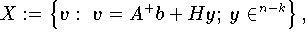
wobei die Spaltenvktoren von
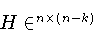 eine Basis des Nullraums
N(A) der Matrix A darstellen.
eine Basis des Nullraums
N(A) der Matrix A darstellen.
Fall 2: 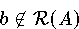
Wenn man den Vektor b nicht als Linearkombination der Spaltenvektoren
von A darstellen kann, so ist 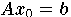 ein widersprüchliches
System..Es gibt in diesem Fall keinen Vektor
ein widersprüchliches
System..Es gibt in diesem Fall keinen Vektor 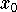 , für den
, für den
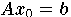 gilt, das Gleichungsystem ist also nicht lösbar.
gilt, das Gleichungsystem ist also nicht lösbar.
Lösung homogener Gleichungssysteme:
Falls die rechte Seite eines linearen Gleichungssysteme der Nullvektor ist, handelt es sich um ein homogenes Gleichungssystem

das für eine Matrix ARnn von allem Rang nur triviale Lösung x=0, für eine singuläre Matrix mit rang(A)=k<n hingegen einen (n-k)-dimensionalen Unterraum N(A) des Rn - den Nullraum von A- als Lösungsmannigfaltigkeit besitzt.
Eine orthogonale Basis des
(n-k)-dimensionalen Lösungsraums N(A) erhält man aus
der Singulärwertzerlegung 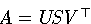 . Mit
. Mit
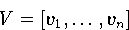 und
und
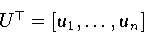 gilt
gilt 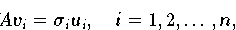 ,
d.h.
,
d.h. 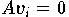 für
für 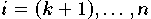 ;
die den Singulärwerten
;
die den Singulärwerten 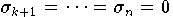 zugeordneten Spaltenvektoren
zugeordneten Spaltenvektoren 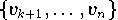 von V
sind die gesuchte orthogonale Basis des Nullraums N(A).
von V
sind die gesuchte orthogonale Basis des Nullraums N(A).
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]