[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Eine n x n Matrix
mit dij = 0 für i <> j wird Diagonalmatrix genannt, mit der Notation
wobei d einen Vektor darstellt, der die Diagonalelemente enthält.
Haben alle Diagonalelemente reelle positive Werte, spricht man von einer positiven Diagonalmatrix. Ein Beispiel dafür ist die Einheitsmatrix:
Eine Diagonalmatrix wird Skalarmatrix genannt, falls alle Diagonalelemente den gleichen Wert haben.
Eine n x n Matrix T = (tij) wird obere Dreiecksmatrix genannt, falls tij = 0 für alle j < i gilt:
Gilt tij = 0 für j <= i , dann nennt man T eine strikte obere Dreiecksmatrix. Analog werden untere und strikte untere Dreiecksmatrizen definiert.
Die Blockung einer Matrix ist eine Zerlegung in disjunkte Untermatrizen. Jedes Element der ursprünglichen Matrix fällt in genau einen Block (eine Untermatrix).
Sei A eine n x n Matrix, 
ist eine
Untermatrix von A, wobei die Menge alpha die Zeilen und die Menge beta
die Spalten der ursprünglichen Matrix A angibt, aus denen
sich die Untermatrix zusammensetzt.
Im Spezialfall 
wird die Untermatrix 
als Hauptuntermatrix
bezeichnet. Oft wird eine Untermatrix auch so angegeben, daß
man jene Zeilen und Spalten, die von der ursprünglichen Matrix
weggelassen werden, anführt.
Die Determinante einer quadratischen Untermatrix von A wird als Minor von A bezeichnet.
Blockdiagonalmatrizen haben die Form
Die Untermatrizen A11,...,Akk sind alle quadratisch, besitzen aber nicht unbedingt alle dieselbe Größe. Viele Eigenschaften von Blockdiagonalmatrizen verallgemeinern die Eigenschaften der Diagonalmatrizen, wie zum Beispiel:
Dementsprechend ist A genau dann regulär, falls alle Aii regulär sind.
Matrizen der Form
sind obere bzw. untere Block-Dreiecksmatrizen. Die Determinante einer solchen Matrix ist durch das Produkt
gegeben. Der Rang von A ist mindestens so groß wie die Summe der Ränge der Diagonalblöcke Aii.
Eine Matrix A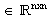 
heißt obere Hessenberg-Matrix,
falls aij = 0 für j+1 < i gilt:
A heißt untere Hessenberg-Matrix, falls AT eine obere Hessenberg-Matrix ist.
Eine Matrix A 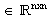, die zugleich eine obere und untere
Hessenberg-Matrix ist, wird tridiagonale Matrix oder Tridiagonalmatrix
genannt. A ist genau dann tridiagonal, falls aij = 0 für
|i-j| > 1 gilt:
Symmetrische Hessenberg-Matrizen sind stets symmetrische Tridiagonalmatrizen.
Bei einer Bandmatrix A 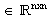sind die von Null verschiedenen
Elemente nur in der Hauptdiagonale a11,...,ann und einigen dazu
parallelen Nebendiagonalen zu finden.
Tridiagonalmatrizen sind spezielle Bandmatrizen mit je einer oberen und unteren nicht verschwindenden Nebendiagonale.
Man bezeichnet P 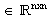als eine Permutationsmatrix, wenn
genau ein Element in jeder Zeile und Spalte den Wert 1 hat und
alle anderen 0 sind. Die Multiplikation PA führt zu einer
Permutation der Zeilen, AP zu einer Permutation der Spalten von
A. Die Determinante det(P) von Permutationsmatrizen ist immer
+/-1, daher sind diese stets regulär. Sie kommutieren nicht
bezüglich der Multiplikation. Das Produkt zweier Permutationsmatrizen
ergibt wieder eine Permutationsmatrix.
PT=P-1 permutiert die Spalten genauso wie P die Zeilen. Die Transformation A -> PAPT permutiert daher die Zeilen und Spalten von A in der selben Weise. Im Zusammenhang mit linearen Gleichungssystemen mit der Koeffizientenmatrix A bedeutet diese Transformation eine Umnumerierung der Variablen.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]