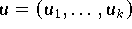 und
und
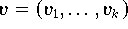 mit
mit
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Zur Definition eines Approximationsproblemes benötigt man eine Distanzfunktion, mit der man quantitative Angaben darüber machen kann, wie weit eine Modellfunktion g von der zu approximierenden Funktion f entfernt ist. Die Wahl der Distanzfunktion D muß den Besonderheiten der jeweiligen Modellierung angepaßt werden. Bei Daten, die mit stochastischen Störungen überlagert sind, wird man z.B. eine andere Abstandsdefinition verwenden als bei ungestörten Daten. Die Wahl der Distanzfunktion beeinflußt auch ganz wesentlich der rechnerischen Aufwand, der zur Ermittlung der Parameter einer Approximationsfunktion erforderlich ist.
Bei der mathematischen Beschreibung von Approximationsprozessen ist es zweckmäßig, Funktionen (Signale) als Punkte oder Vektoren in einem Funktionenraum (Signalraum), (Signal-) transformationen als Abbildungen dieses Raumes und Eigenschaften der Funktionen als Eigenschaften der Raumes zu betrachten. Der Begriff "Raum" wird benützt, um der Funktionenmenge eine geometrische Anschaulichkeit zu verleihen.
Nachfolgende Definitionen sind für das Verständnis des Nachfolgenden Kapitels Voraussetzung:
Bei Normen kann man zwischen:| Normen für endlich-dimensionale Räume | |
| und | Normen für unendlich-dimensionale Räume |
Gewichtete Normen gehen davon aus, daß nicht jeder Funktionswert die gleiche Bedeutsamkeit besitzt.
Im Raum der diskreten binären Signale verwendet man oft die
Hamming-Distanz zweier Binärvektoren
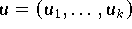 und
und
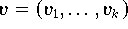 mit
mit
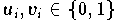
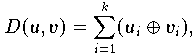
die sich aus der Anzahl der unterschiedlichen Komponenten in u und v ergibt:
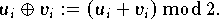
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]