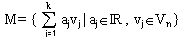 aller Linearkombinationen der
Vektoren v1,...,vk
aller Linearkombinationen der
Vektoren v1,...,vk  Vn
Vn
ist ein Unterraum von Vn und heißt die lineareHülle von v1,...,vk
Das heißt, man nimmt k Vektoren aus V und bildet alle möglichen Linearkombinationen.
[ < ] [ globale Übersicht ][ Kapitelübersicht ][ Stichwortsuche ][ > ]
Wir setzen n für die Dimension des Vektorraumes.
Lineare Hülle, Lineare Unabhängigkeit, Basis, Dimension:
Definition "Lineare Hülle"
Die Menge 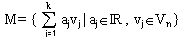 aller Linearkombinationen der
Vektoren v1,...,vk
aller Linearkombinationen der
Vektoren v1,...,vk  Vn
Vn
ist ein Unterraum von Vn und heißt die lineareHülle
von v1,...,vk
Das heißt, man nimmt k Vektoren aus V und bildet alle möglichen Linearkombinationen.
Definition "Lineare Unabhängigkeit von Vektoren"
Die Vektoren v1,...,vk  Vn
heißen linear unabhängig, wenn
Vn
heißen linear unabhängig, wenn 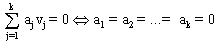 gilt,
sonst linear abhängig.
gilt,
sonst linear abhängig.
Das heißt, der Nullvektor läßt sich nur durch alle
Koeffizienten gleich 0 darstellen.
Definition "Basis von V"
Eine Teilmenge B des Vektorraumes V keißt Basis von V, wenn:
1) B linear unabhängig ist und
2) die lineare Hülle von B gleich V ist.
Das heißt, man prüft als erstes, ob B sich nur als Linearkombination
mit allen Koeffizienten gleich 0 darstellen läßt. Danach
schaut man, ob dieses System den Vektorraum V erzeugt, wenn man
alle möglichen Werte für die Koeffizienten einsetzt.
Wenn ja, ist B eine Basis.
---> Siehe auch kanonische Basis .
Wenn man einen bestimmten Vektor durch eine Linearkombination der
Basisvektoren darstellt, nennt man die dabei auftretenden Koeffizienten
die Koordinaten von V bezüglich einer Basis.
Definition "Dimension"
Die Anzahl der Vektoren der Basis ist die Dimension von V.
d.h. |B| = dim V
Definition "kanonische Basis(natürliche Basis)"
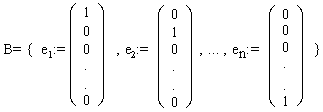 heißt kanon. Basis.
heißt kanon. Basis.
Das sind n Einheitsvektoren. Sie bilden eine Basis des Vn. Jeder Vektor des Vn kann durch Koeffizienten der Linearkombination von B dargestellt werden.
Vektornormen, Orthogonalität, Lineare Funktionen:
Definition Norm (Matrixnorm)
Eine Abbildung ||.|| :  mxn
mxn
 , die für alle
A , B
, die für alle
A , B 
 mxn
den Bedingungen
mxn
den Bedingungen
1.||A|| < = 0,
2.||A|| = 0 <==> (Definitheit)
3.||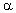 A|| = |
A|| = |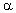 |*
||A|| ,
|*
||A|| , 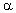

 (Homogenität)
(Homogenität)
4.||A+B|| <= ||A|| + ||B|| (Dreiecksungleichung)
genügt, heißt Norm (Matrixnorm). Für die Vektornorm nimmt
man einfach  1xn also
1xn also n.
Die Vektornorm ist also ein Spezialfall der Matrixnorm.
n.
Die Vektornorm ist also ein Spezialfall der Matrixnorm.
Unter einer Vektornorm versteht man, vereinfacht gesagt, die Länge eines
Vektors. Egal, wie groß die Dimension des Vektorraumes ist,
die Norm bildet einen Vektor auf ein Skalar ab. Diese Länge kann
man jedoch unterschiedlich definieren.
-->Siehe auch endlich-dimensionale Normen
Die zwei wichtigsten Normen sind die euklidische Norm und die Maximumnorm.
Wenn p=2, dann spricht man von der Euklidischen Norm. Sie ist die
Wurzel des skalaren Produkts.
d.h. ||x||2 :=
Wenn p=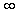 ,dann spricht man von der Maximumnorm.
,dann spricht man von der Maximumnorm.
d.h. ||x||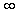 := max {|u1-v1|,...,|un-vn|}
:= max {|u1-v1|,...,|un-vn|}
Definition Norm - Äquivalenz
Unter der Norm-Äquivalenz versteht man:
Für zwei beliebige Normen ||.|| und ||.||'auf
dem  n existieren Konstanten c2>=c1>0,
sodaß folgende Ungleichung gilt:
n existieren Konstanten c2>=c1>0,
sodaß folgende Ungleichung gilt:
c1||x||<=||x||'<=c2||x||
Das heißt:
Die Abstände aller Vektoren ,mit einer bestimmten Norm berechnet, sind
alle kleiner gleich oder alle größer gleich als die
Abstände mit einer anderen Norm, multipliziert mit einem konstanten
Faktor.
Beispiel:
Für die Vektornormen ||.||1 , ||.||2 und
||.||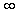 gilt für
alle x
gilt für
alle x
 n:
n:
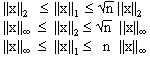
Wie man aus diesen Ungleichungen sieht, können die Konstantenc1 und c2 unter Umständen auch von der Dimension n abhängen.
Definition: "Skalarprodukt (Innere Produkt) zweier Vektoren
" u,v 
 :
:
< u , v > = uTv = u1v1+u2v2+...+unvn
Definition "Winkel zweier Vektoren"
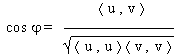
Wenn u und v eine Winkel von 90° einschließen, so gilt < u , v > = 0
Definition "Orthogonalität , Orthogonalsystem"
Zwei Vektoren heißen orthogonal, wenn < u , v
> =0 gilt, d.h. wenn sie normal aufeinander stehen. Die Vektoren u1,...,uk

 nheißen
orthogonal, wenn sie paarweise orthogonal sind. Die Menge {u1,...,uk}
heißt Orthogonalsystem.
nheißen
orthogonal, wenn sie paarweise orthogonal sind. Die Menge {u1,...,uk}
heißt Orthogonalsystem.
Definition "Orthonormalsystem"
Ist bei einem Orthogonalsystem bei jedem Vektor die euklidische Länge
gleich 1 (=normierter Vektor) , gilt also:
||ui||2 = 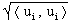 = 1,
i=1,2,...k
= 1,
i=1,2,...k
so heißt dieser Spezialfall Orthonormalsystem.
Definition "Orthogonales Komplement"
Das orthogonale Komplement eines Teilraumes S des  nist die Menge S
nist die Menge S ={ v
={ v 
 n | < u , v >=0 f.a.u
n | < u , v >=0 f.a.u
 S}
S}
die selbst Teilraum des  nist.
nist.
S besteht also nur aus Vektoren,
die normal auf Vektoren v
besteht also nur aus Vektoren,
die normal auf Vektoren v  V sind.
V sind.
Definition "Schmidtsches Orthonormalisierungsverfahren"
Jede Menge {a1,....,ak} linear unabhängiger Vektoren kann nach dem Schmidtschen Verfahren orthonormalisiert werden. Man beginnt dabei mit dem Vektor a1 , der normiert wird:
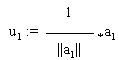
Subtrahiert man von a2 die Komponente, die in Richtung von
u1 weist, so erhält man mit
v2:=a2-<a2, u1>*u1
einen zu u1 orthogonalen Vektor.
Durch Normieren erhält man
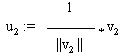
Den dritten orthogonalen Vektor erhält man analog durch
v3:=a3-< a3,u1>*
u1 - < a3,u2> * u2
Allgemein hat das Schmidtsche Verfahren folgende algorithmische Struktur:
u1:=a1 / ||a1||
do i = 2,3,...,k
vi:=ai- 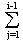 <ai,
uj> *uj
<ai,
uj> *uj
ui:= vi / ||vi||
end do
Definition "lineare Funktion (lineare Abbildung)"
Eine Funktion F: Xn  Ynmit Eigenschaften:
Ynmit Eigenschaften:
1) F(x1+x2) = F(x1) + F(x2)für
alle x1,x2,  Xn
:Additivität
Xn
:Additivität
2) F(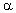 ) =
) = 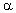 F(x)f.a.
x
F(x)f.a.
x  Xn ,
Xn , 
 :Homogenität
:Homogenität
heißt lineare Funktion oder lineare Abbildung.
Gilt n<=m und X ist ein System linear unabhängiger Vektoren, so ist auch Y ein System linear unabhängiger Vektoren.
Definition "Kern (Nullraum)"
N(F):={ x: F(x)=0} 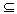 Xn
Xn
Das heißt, alle Vektoren  X , die auf
den Nullvektor abgebildet werden.
X , die auf
den Nullvektor abgebildet werden.
Definition: "Defekt"
Die Dimension des Kerns heißt Defekt.
Definition: "Bildraum"
Die Menge aller Bildvektoren heißt Wertebereich oder Bildraum.
Definition "Rang"
Die Dimension der Abbildung F(U) heißt Rang von F.
Jeden Vektor x kann man eindeutig als Linearkombination darstellen:
x = 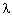 1u1 +
1u1 + 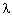 2u2
+ ... +
2u2
+ ... + 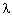 nun
nun
wobei u1,...,un die Basisvektoren sind.
Bildet man nur einen Basisvektor von U auf V ab, so kann man diesen abgebildeten Vektor wieder als Linearkombination darstellen, also:
F(u1) = a11v1 + a21v2+ ... + am1vm
wobei die Basisvektoren aus V sind.
Bildet man nun jeden Basisvektor von U auf V ab, so erhält man
eine Matrix mit Koeffizienten aus V. Diese Koeffizienten charakterisieren eindeutig
die lineare Funktion:
F(u1) = a11v1 + a21v2+
... + am1vm
F(u2) = a12v1 + a22v2+
... + am2vm
..... ..... ..... ..... .....
F(un) = a1nv1 + a2nv2+
... + amnvm
Die Matrix einer lineare Abbildung bildet also die Basisvektorenvon
U auf V ab.
Definition "Matrix einer linearen Abbildung"
Sei A eine Matrix.
...............| a11 a12 ..... a1n
|
...............| a21 a22 ..... a2n
|
A=(aij) = |.........................|
...............| am1 am2 ... amn
|
mit aij  V.
V.
Das heißt, mit einer solchen Matrix läßt sich jede
lineare Funktion von U in V beschreiben.
Bei der Lösung eines linearen Gleichungssystems ist das Urbild gesucht
und die lineare Funktion und das Abbild gegeben.
Also: Ax = b , wobei A und b gegeben ist und x gesucht ist. (b und
x sind Vektoren !)
Dabei schreibt man in jede Zeile der Matrix die Koeffizienten einer
Gleichung, während b jeweils die dazugehörige "rechte
Seite" enthält, also eine Konstante.
Zur Lösung dieses Gleichungssystems siehe LU - Zerlegung
Oft will man die Matrix einer linearen Abbildung bezüglich der
kanonischen Basis bestimmen.
also mit 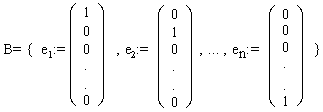


Beispiel:
Sei U =  3 , V =
3 , V =  2
2
Definition Rang einer Matrix
rang(A) einer Matrix ist die größte Anzahl linear unabhängiger Spaltenvektoren.
Definition Rangverlust einer Matrix
N(A)={x : Ax=0 , x
 n}
n}
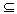
 n
n
Die Dimension des Nullraumes heißt Rangverlust oder Defekt der Matrix A.
Für rang(A)=k (k steht für k x k Matrix) und für rang(A)=n
(n steht für Dimension vom Urbild) gibt es mehrere äquivalente
Aussagen:
rang(A)=k:
1. rang(A)=k
2. Es existieren genau k linear unabhängige Zeilenvektoren von A
3. Es existieren genau k linear unabhängige Spaltenvektoren von A
4. Der Defekt N(A) ist n-k
rang(A)=n:
1. rang(A)=n
2. A ist regulär.
3. A-1 existiert.
4. det(A)<>0
5. Die Zeilenvektoren von A sind l.u.
6. Die Spaltenvektoren von A sind l.u.
7. Der Rangverlust ist 0.
8. Ax=b ist konsistent für alle b
 n.
n.
9. Ax=b hat eine eindeutige Lösung für jedes b
 n
n
Wenn jedes der linearen Gleichungssysteme
Ax1=e1 , Ax2=e2, ...,Axn=en
mit A 
 nxn und
den Einheitsvektoren als rechten Seiten eine eindeutige Lösung x1*
,...,xn* (bestimmtex* !) besitzt,
dann kann man diese Lösungsvektoren als Spaltenvektoren einer
n x n -Matrix
nxn und
den Einheitsvektoren als rechten Seiten eine eindeutige Lösung x1*
,...,xn* (bestimmtex* !) besitzt,
dann kann man diese Lösungsvektoren als Spaltenvektoren einer
n x n -Matrix
X:=[x1* , x2* , ...,
xn*]
auffassen. Diese Matrix, die AX = I erfüllt, wird Inverse von
A genannt und mit A-1 bezeichnet. Wird die Inverse in
Formeln verwendet, so wird sie nicht explizit berechnet. Das führt
sowohl bezüglich des Rechenaufwandes als auch der Genauigkeit
der Resultate zu einem ungünstigen Lösungsweg.
Beispiel:
Man möchte folgende Formeln ausrechnen:
y = B-1 (I+3A)b , z = A-1(2B+I)(C-1+B)b
Man berechnet dabei nicht A-1 , B-1 und C -1 , sondern geht folgenden Lösungsweg:
w:=(I+3A)b
solve By=w
solve Cu=b
v:= (2B+I)(u*+Bb)
solve Az=v
Die Inverse wird also praktisch nie benötigt.
Definition "Norm einer Matrix"
Die Definition der Matrixnorm ist die Definition der Norm.
Genauso wie bei den Vektoren, kann man auch bei den Matrizen eine Norm definieren, also den Abstand zweier Matrizen berechnen. Diese bildet eine Matrix auf ein Skalar ab. Die wichtigste ist die p-Norm. Dabei wird die Matrix mit allen Vektoren für die gilt : x:||x||p=1 multipliziert. Das Ergebnis sind Vektoren.Sie werden wieder alle normiert. Der größte ,jetzt ein Skalarwert, ist die Norm der Matrix.
Also:
||A||p = 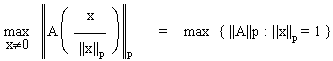
Im Einzelnen nun die wichtigsten Matrixnormen:
Spaltensummennorm:
||A||1 = max { 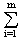 |aij|:
j = 1 ,..., n}
|aij|:
j = 1 ,..., n}
Zeilensummennorm:
||A||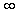 = max {
= max { 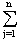 |aij|:i=
1 ,..., m}
|aij|:i=
1 ,..., m}
Euklidische oder Spektralnorm:
||A||2 = 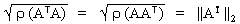
Man verwendet ATA statt A um reele Eigenwerte zu bekommen.
Weil ATA symmetrisch ist,ist es gleich AAT.
Die Berechnung von ||x||1 und ||A|| benötigt
nur n2 Additionen, während die Berechnung von ||A||2
einen größeren Rechenaufwand hat (Matrixmultiplikation
!).
benötigt
nur n2 Additionen, während die Berechnung von ||A||2
einen größeren Rechenaufwand hat (Matrixmultiplikation
!).
Die übliche Definition der Determinante ist folgende:
Definition Determinante
Die Determinante einer quadratischen Matrix A 
 nxn ist eine Abbildung:
nxn ist eine Abbildung:
det:  nxn
nxn 
 ,
,
die folgendermaßen definiert ist:
det (A) := 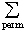 sign(v1,....,vn)a1v1a2v2...anvn
sign(v1,....,vn)a1v1a2v2...anvn
Dabei ist die Summe über alle n! Permutationen (v1,...,vn)der
Zahlen 1,...,n zu erstrecken.
sign(v1,...,vn) kann entweder +1 (gerade Permutation) oder -1(ungerade
Permutation) sein, bestimmt also das Vorzeichen der folgenden Multiplikation.
Diese Definition eignet sich aber nicht für die praktische Berechnung von det(A) weil sie einen Aufwand von O(n!) hat. Man verwendet ein anderes Verfahren, nämlich die LU - Zerlegung, die Determinante als "Nebenprodukt" liefert und O(n³) Aufwand hat.
Außerdem eignet sie sich nicht für ein praktisch einsetzbares Kriterium für die Lösbarkeit eines linearen Gleichungssystems.Durch die vielen Multiplikationen entstehen unvermeidbare Rundungsfehler. Daher kann man det(A)=0 als Kriterium für die Singularität nicht verwenden. Auch wenn das Ergebnis in der Nähe von Null ist , gibt das keinen Hinweis auf Singularität.
Der Grund für dieses Verhalten ist die folgende Eigenschaft von
der Determinante :
det(cA) = cn.det (A)
Das heißt, multipliziert man eine Matrix mit einer Konstante und
berechnet dann die Determinante, so ist das Ergebnis gleich Konstante
hoch Dimension mal die Determinante von A alleine.
Eine Multiplikation aller Elemente der Matrix hat also auch eine kleine
Multiplikation der Determinante zufolge. Diese sollte Null sein,
wenn A singulär ist. Durch Multiplizieren der Matrix mit einer
Konstanten sollte sich daran nichts ändern. Durch die Rundungsfehler
kommt allerdings nicht genau Null heraus und wird durch die Konstante
noch mal verfälscht.
[ < ] [ globale Übersicht ][ Kapitelübersicht ] [ Stichwortsuche ][ > ]