[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Zu jeder gegebenen Funktion oder diskreten Punktmenge gibt es eine unendliche Menge G von Approximationsfunktionen, z.B. die Menge aller reellwertigen Funktionen, die an bestimmten Stellen mit den Datenpunkten übereinstimmen oder einen - noch näher zu präzisierenden - endlichen Abstand von den Datenpunkten besitzen (siehe Wahl der Distanzfunktion - Abschnitt 6.4). Die Menge G besitzt im allgemeinen sowohl eine unendliche Teilmenge von "guten" als auch eine unendliche Teilmenge von "schlechten" Approximationsfunktionen. Es erhebt sich daher die Frage, nach welchen Kriterien man in G nach "möglichst guten" Approximationsfunktionen suchen soll.
In den folgenden Abschnitten werden Aspekte beleuchtet, die bei der Auswahl von Apprixomationsfunktionen von Bedeutung sind (vgl auch die Zusammenstellung von Brodlie [131]). Die Bewertung der Eigenschaften verschiedener Darstellungsfunktionen und die eigentliche Auswahl kann jedoch nur im speziellen Anwendungsfall vorgenommen werden.
Es gibt zwei Möglichkeiten der Definition einer Approximationsfunktion:
Wenn es das Ziel der Approximation ist, ein möglichst unkompliziert zu berechnendes und einfach handhabbares Modell zu erhalten, wäre es naheliegend, z.B. an die Verwendung eines einzigen (global definierten) Polynoms zu denken. Nach dem Satz von Weierstraß ({!}Satz 9.3.4{!}) gibt es zu jeder geforderten Genauigkeit (im Sinne der Maximalabweichung) ein Polynom, das dieser Anforderung genügt, vorausgesetzt, die zu approximierende Funktion ist auf B. Obwohl duese Aussage mathematisch korrekt ist, darf man jedoch nicht annehmen, damit alle praktischen Probleme lösen zu können (siehe Kapitel 6.6 ff).
In vielen Fällen, etwa bei stark oszillierendem Verhalten oder "uneinheitlichem" Funktionsverlauf (mit sehr glatten Abschnitten und Stellen mit extrem starker Krümmung, z.b. "Spitzen", "Ecken", etc.) kann ein dem Weierstraßschen Satz entsprechendes Approximationspolynom - auch bei einer bescheidenen Genauigkeitsforderung - unter Umständen einen extrem hohen Grad besitzen. Welche Polynomgrade man in welchen Fällen als "hoch" (bzw. "zu hoch") anzusehen hat, wird in den folgenden Abschnitten und Kapiteln besprochen.
Aus den genannten Gründen erweist es sich oft als ungünstig, die Approximationsaufgabe mit einem Polynom eines hohen Grades auf dem gesamten Bereich B zu lösen. Die effizientere Lösung besteht in vielen Fällen in der Zerlegung von B in disjunkte Teilbereiche B1, B2, ..., Bm, auf denen jeweils ein separates Approximationspolynom niedrigeren Grades bestimmt.
Eine der fundamentalsten Entscheidungen bei der Wahl einer Klasse von Modellfunktionen (Approximationsfunktion)
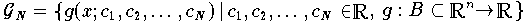
betrifft ihre Linearität. Dabei muß sorgfältig auseinandergehalten werden:
Die meisten Vorgänge und Zusammenhänge der realen Welt sind nichtlinear. Dennoch besitzen Modelle, die linear in x sind, in vielen praktisch relevanten Fällen eine zufriedenstellende, manchmal sogar sehr hohe Aussagekraft.
[BEISPIEL: Elektrische Stromkreise]
Viele mathematischen Untersuchungs- und Lösungsmethoden (analytische und numerische) sind besser und manchmal sogar ausschließlich für lineare Problemstellungen geeignet. Dieser Umstand führt zur Anwendung linearer Modelle sogar in jenen Fällen, wo es ernsthafte Gründe für die Annahme gibt, daß sich die reale Abhängigkeit wesentlich von einer linearen unterscheidet.
Die Fehler, die durch das Ersetzen einer nichtlinearen Abhängigkeit durch eine lineare gemacht werden, können quantitativer oder qualitativer Art sein. Im ersten Fall beschreibt die Lösung der mathematischen Aufgabe die Eigenschaften des realen Vorganges im großen und ganzen richtig, obwohl es konkrtet numerische Ergebnisse gibt, die vor den wahren Werten stark abweichen. Im zweiten Fall werden einige in Wirklichkeit beobachtbare Effekte durch das lineare Modell überhaupt nicht wiedergegeben. Solche Effekte nennt man "wesentlich nichtlinear", für ihre Wiedergabe sind lineare Modelle prinzipell ungeeignet. Typische Beispiele für wesentlich nichtlineare Effekte sind Sättigungserscheinungen, Verzweigungen, Chaos etc. In solchen Fällen müssen nichtlineare Modelle verwendet werden.
Ob man von einer linearen oder nichtlinearen Approximationsmethode spicht, hängt nicht von der Art der Abhängigkeit der
Funktion g von ihrer unabhängigen Variablen x, sondern von der Art der Abhängigkeit der Approximationsfunktion g von ihren
Parametern
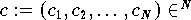
ab.
Definition 6.3.1 (Lineare Approximation) Eine Approximationsfunktion g nennt man linear, wenn sie additiv und homogen bezüglich ihrer Parameter ist, also folgende Eigenschafen besitzt:
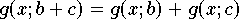(Additivität) 
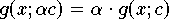(Homogenität). So führt z.B. die Verwendung von Polynomen
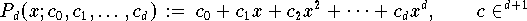
als Modellfunktionen in diesem Sinn auf lineare Approximationsprobleme.
Lineare Approximationsfunktionen können stets als Linearkombinationen von festen, gegbenen (linear unabhängigen) Basisfunktionen
dargestellt werden:
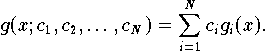
[BEISPIEL: Polynome], [BEISPIEL: Trigonometrische Polynome]
In diesem Fall wird der Definitionsbereich B in Teilbereiche B1, B2, ..., Bm zerlegt, und g ist auf jedem Teilgebiet eine lineare Approximationsfunktion:
{FORMEL 11}
Die Eigenschaft der Additivität erleichtert unter anderem die Durchführung experimenteller Sensitivitätsuntersuchungen, ei denen man ausgewählte Datensätze mit additiven Störungen überlagert und deren Auswirkungen auf die Approximationsfunktion studiert.
In der Praxis treten meist gemischt linear-nichtlineare Modellfunktionen auf:
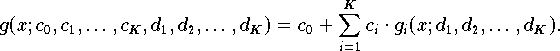
Dabei sind c0, ..., ck die linearen und d0, ..., dk die nichtlinearen Parameter. Haben die nichtlinearen Parameter von Anfang an bekannte Werte, dann handelt es sich auch hier um ein lineares Approximationsproblem.
Vergleicht man die Eigenschaften von linearen und nichtlinearen Approximationsfunktionen, so ergibt sich aus mathematisch-algorithmischer Sicht ein klarer Vorteil für die linearen Approximationsfunktionen. Es gibt jedoch Situationen, in denen man gezwungen ist, nichtlineare Approximationsfunktionen zu verwenden:
Bei
globalen Approximationsmethoden
hängt der Wert der Approximationsfunktion g an jeder beliebigen Stelle x 
B von
allen Datenpunkten ab. Dementsprechend ist auch die Kenntnis aller Datenpunkte für die Ermittlung der Parameter c1, c2, ...,
cn erforderlich. Polynominterpolation (mit einem durchgehenden Polynom) und kubische Spline-Interpolation sind Beispiele für
solche globalen Approximationsmethoden.
Bei der globalen Approximation wirkt sich die Änderung (Störung) eines einzelnen Datenpunktes auf den gesamten Funktionsverlauf aus. Auch an Stellen, die weit vom Ort der Änderung entfernt sind, kann sich die Funktion unter Umständen sehr stark verändern.
Bei lokalen Approximationsmethoden hängt die Approximationsfunktion zwischen zwei Datenpunkten nur von diesen beiden und eventuell einigen weiteren Datenpunkten aus der unmittelbaren Umgebung ab. Diese Eigenschaft ermöglicht die Ermittlung von Teilen der Approximationsfunktion ohne Kenntnis der Gesamtmenge der Datenpunkte.
Bei der lokalen Approximation kann sich die Änderung (Störung) eines Datenpunktes nur auf dessen unmittelbare Umgebung auswirken (siehe Abb.8.9),
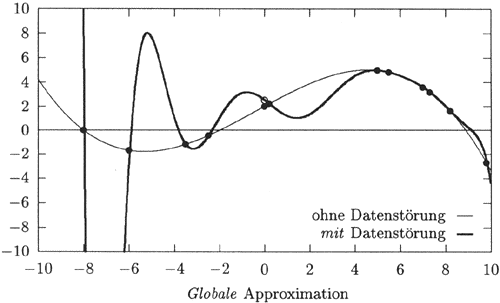
Abb 6.8: Interpolation der Datenpunkte (O) durch ein Interpolationspolynom führt zu extremen Schwingungen, wenn auch nur ein Datenpunkt, hier jener an der Stelle x = 0 von y = 2 auf y = 2.5 verschoben wird (o). Alle anderen Datenpunkte (insbesondere der Nachbarpunkt mit x = 0.2 und y = 2.2) bleiben unverändert.
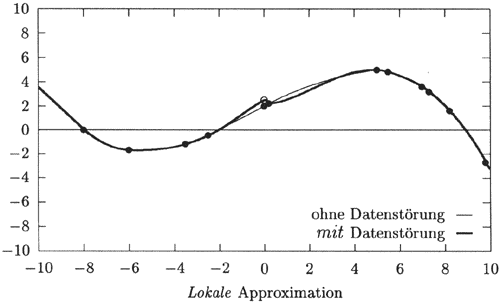
Abb 6.9: Interpolation derselben Datenpunkte (O) wie in Abb 6.8 durch eine stückweise definierte Akima-Funktion weist auch bei einem in y-Richtung verschobenen Datenpunkt (o) nahezu kein Überschwingen auf.
[BEISPIEL Stückweise kubische Funktionen]
Ein algorithmischer Vorteil der lokalen Approximationfunktionen ergibt sich aus dem vergleichsweise sehr geringen Rechenaufwand, der auf die entkoppelten Gleichungssysteme zur Bestimmung der Parameter zurückzuführen ist. Durch diese Entkopplung eignen sich lokale Approximationsverfahren in natürlicher Weise besonders gut für {!}Parallelrechner{!}.
Lokale Verfahren können mit durchgehend definierten Approximationsfunktionen nicht realisiert werden; als Approximationsfunktionen kommen für lokale Verfahren nur stückweise (intervallweise) definierte Funktionen in Frage. Es führt aber umgekehrt die Verwendung stückweise definierter Funktionen nicht in jedem Fall auf lokale Verfahren, wie das Beispiel der kubischen Splinefunktionen zeigt (siehe Abschnitt 9.7)
Stetigkeits- und Differenzierbarkeitseigenschaften sind mathematische Charakteristika der "Glattheit" einer Funktion . Je öfter eine Funktion (stetig) differenzierbar ist, desto glatter ist sie im mathematischen Sinn.
[BEISPIEL Polygonzug], [BEISPIEL Kubische Splines], [BEISPIEL Polynome]
Polynome sind durch ihre beliebig oftmalige Differenzierbarkeit sehr glatt im mathematischen Sinn. Dies trifft aber keinesfalls auch immer auf ihren optischen Eindruck zu, wie er etwa bei Visualisierungs-Anwendungen wichtig ist. Speziell bei Polynomen mit "hohem" Grad (das kann - je nach Anwendungfall - schon d >= 10 sein) tritt oft starkes Oszillieren - "Überschwingen" - und damit ein visuell "nicht-glattes" Erscheinungsbild auf (siehe Abb 8.8 und Abb 8.12)
Polygonzüge sind im mathematischen Sinn nicht glatt. Soferne man jedoch die Abstände der Knotenpunkte xi+1 - xi an den Verlauf der zu approximierenden Funktion f anpassen kann, ist es immer möglich, einen Polygonzug g zu finden, der sich optisch (innerhalb der Auflösung des Darstellungsmediums) nicht von f unterscheiden läßt.
Da es bei Approximationsproblemen - je nach Aufgabenstellung - auf die Modellfunktion oder deren Parameter ankommt, gibt es zwei Konditionsbegriffe:
Kondition der Funktionswerte: Die Konditionszahl kf charakterisiert die Empfindlichkeit der Werte der
Approximationsfunktion gegen Datenänderung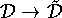 
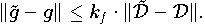
Kondition der Parameter: Die Konditionszahl kc charakterisiert die Empfindlichkeit der Parameter der Approximationsfunktion
gegen Datenänderungen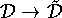
Die Größe der Konditionszahlen kf und kc hängt nicht nur vor der Kondition des Approximationsproblems ab, sondern auch von der Wahl der Normen in den Ungleichungen (8.7) und (8.8) (vgl. Abschnitt 6.4).
[BEISPIEL: Interpolation mit Polynomen]
Obwohl eine spezielle Form der Approximationsfunktion g durch theoretische Überlegungen oder numerische Resultate stark untermauert sein kann, treten Fälle auf, bei welchen sich die Parameter der Approximationsfunktion aus den Daten nur mit großer Unsicherheit bestimmen lassen. So ist z.B. die Parameterbestimmung von Exponentialsummen ein notorisch schlecht konditioniertes Problem, während die Funktionsauswertung von Exponentialsummen durchaus gut konditioniert ist.
[BEISPIEL Approximation mit Exponentialsummen]
Abb. 6.10: (Fehlerdarstellung) Die Abweichung der Näherungsfunktion g von den diskretisierten und quantisierten Datenpunkten (O) der ursprünglichen Funktion f(t) und die Abweichung der Näherungsfunktion g(t) von f(t) (-) liegen beide in der Größenordnung der Datenfehler.
Die Eigenschaft der Invarianz unter Skalierungstransformationen ist z.B. in der graphischen Datenverarbeitung von Bedeutung. Im jeweiligen Anwendungsgebiet definiert man zunächst alles graphisch Darzustellende in zweidimensionalen kartesischen Koordinaten, die Weltkoordinaten genannt werden. Die Normalisierungstransformation
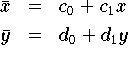
bildet (mit geeigneten Konstanten c0, c1, d0, d1) den Weltkoordinatenbereich auf den normalisierten Koordinatenbereich [0,1]x[0,1] ab. Die Gerätetransformation
{FORMEL 19}
bildet schließlich den normalisierten (geräteunabhängigen) Koordinatenbereich auf den Gerätekoordinatenbereich eines konkreten graphischen Arbeitsplatzes ab (Salmon, Slater [352]). Ein Verfahren, das unter Skalierungstransformationen invariant ist, liefert in diesem Fall denselben Funktionsverlauf, gleichgültig, ob der Approximationsalgorithmus auf Welt- oder (normalisierte) Gerätekoordinaten angewendet wird. Diese Eigenschaft erleichtert z.B. die Entwicklung von Black-Box-Visualisierungsprogrammen, bei denen der graphische Output nicht von Implementierungsdetails abhängt.
Wenn das zu modellierende kontinuierliche Phänomen bzw. Die verfügbaren Daten - speziell im univariaten Fall - bestimmte Formeigenschaften aufweisen (z.B.Monotonie, Konvexität, eine bestimmte Anzahl von Wendepunkten), so kann an die Approximationsfunktion die Forderung gerichtet werden, diese Eigenschaften ebenfalls zu besitzen.
Wenn die Approximationsfunktion die Formeigenschaften der Daten nicht besitzt, so ist oft "Überschwingen" dafür verantwortlich. Die Approximationsfunktion weist ein oszillierendes Verhalten auf, obwohl dies bei den Daten nicht zu beobachten ist (z.B. bei monotonem Datenverlauf; siehe Abb 8.11 und Abb 8.12).
Einbringen von Information über die erwartete Lösung in Form von Nebenbedingungen des Approximationsproblems führt oft zu einer erheblichen Konditionsverbesserung. Diese Vorgangsweise bezeichnet man als Regularisierung. "Überschwingen" kann durch geeignete - dem Modellierungsproblem angemessene - Nebenbedingungen (etwa duch eine Monotonie-Forderung) vollständig vermieden werden.
In manchen Fällen wird eine Modellfunktion gesucht, die an bestimmten Punkten vorgegebenen Werte annimmt oder deren Ableitungen an diesen Stellen bestimmte Werte annehmen. So wird z.B. von einer Approximationsfunktion, die in einem Standardfunktionsunterprogramm für sin(x) Verwendung finden soll, erwarten, daß sie an der Stelle x = 0 exact den Wert 0 liefert, an der Stelle x = {[PI]}/6 den Wert 0.5 etc. Wenn man das Approximationsproblem nach dem Interpolationsprinzip löst, genügt es, diese speziellen Abzissen den Interpolationsknoten hinzufügen. Bei Anwendung des Bestapproximationsprinzips muß man diesen Nebenbedingungen durch eine Änderung des Approximationsalgorithmus Rechnung tragen. Bei Polynomapproximation kann dies z.B. durch die Wahl einer speziellen Form des Polynoms erreicht werden (Hayes [229], Kapitel 5):
{FORMEL 20},
wobei PR ein Polynom ist - üblicherweise von kleinstmöglichem Grad - das die Nebenbedingungen erfüllt, und PK ein Polynom, für das
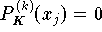
an allen Stellen xj gilt, an denen die k-te Ableitung (k >= 0) der Approximationsfunktion einer Nebenbedingung unterworfen wurde.
[BEISPIEL Polynom mit Nebenbedingungen]
Nebenbedingungen beziehen sich oft nicht nur auf einzelne Punkte, sondern auf das gesamte Gebiet B oder (meist
intervallförmige) Teilmengen Br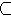 
B. Es handelt sich dabei meist um Einschränkungen für die Ableitungen der
Approximationsfunktion:
Die praktisch wichtigsten Fälle sind:
Beschränkung der Funktionswerte (k = 0):
z.b. Anteile oder Konzentrationen, die nur zwischen m = 0 und M = 1 bzw. zwischen 0% und 100% liegen können;
Monotonie (k = 1):
z.B. akkumulierte Größen, die nicht abnehmen können (siehe Abb. 6.11);
Konverxität (k = 3):
konvexer Funktionsverlauf: {FORMEL 25}
konkaver Funktionsverlauf: {FORMEL 26}
Die algorithmische Lösung von Approximationsproblemen mit Nebenbedingungen erfordert den Einsatz von Verfahren für restringierte Minimierungsprobleme (constrained minimization). Eine Übersicht über die Programmpakete für diesen Problemtyp findet man im Buch von Moré und Wright [21].
Für spezielle Funktionenklassen gibt es oft sehr effiziente Algorithmen und Programme: Verfahren für konvexe Splinefunktionen findet man z.B. bei de Boor [40], Shumaker [364], Andersson und Elfving [87]; Algorithmen für monotone Splinefunktionen z.B. bei Fritsch und Carlson [208], Fritsch und Butland [207], Hyman [243], Constantini [147].
Neben den mathematisch formulierbaren Eigenschaften einer Funktion gibt es auch ein subjektives Formempfinden. Die visuelle Beurteilung einer Approximationsfunktion beruht meist auf schwer formalisierbaren Vorstellungen über die "passende" Approximationsfunktion. Diese unbewußten Vorstellungen deckensich oft mit jenem Funktionsverlauf, den der Betrachter bei einer Freihandzeichnung wählen würde, bei der er Vorhandene Vorinformation (wie z.B. Monotonie, Konvexität, Nichtnegativität, etc.) berücksichtigt.
Manche Approximationsarten kommen den subjektiven Formvorstellungen eher entgegen als andere. So empfinden z.B. bei der Akima-Interpolation ({!}Akima [82]{!}) viele Personen eine wesentlich größere Ähnlichkeit zu einer Freihandzeichnung als bei der Interpolation mit einem durchgehenden Polynom hohen Grades (bei den Kurven in Abb 8.12 ist dies besonders offensichtlich)
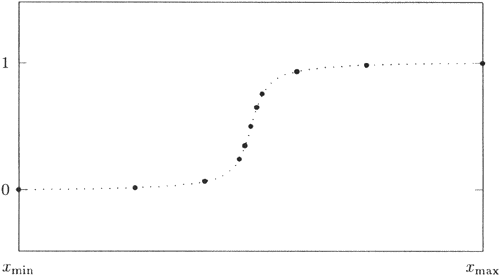
Abb 6.11: Datenpunkte (O) einer Sättigungsfunktion (...)
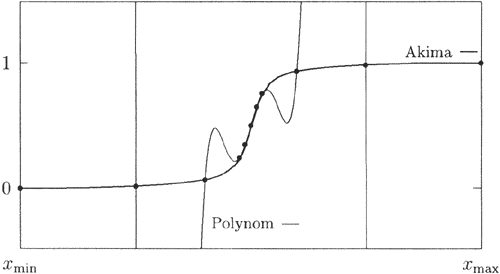
Abb. 6.12: Interpolation der Datenpunkte von Abb 6.11 durch ein Interpolationspolynom von Grad 10 (-) und durch eine stückweise kubische Akima-Funktion (-).
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
