Markus Spöttl

Schwarzinger Rainer

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

6.6 Allgemeines zur Interpolation

Allgemeines

Dem Prozeß der Interpolation liegen als Daten k Punkte <em>x</em><sub>1</sub>, <em>x</em><sub>2</sub>, ..., <em>x</em><sub>k</sub> {[Element]} <em>R</em><sup><em>N</em></sup> - die sogenannten Interpolationsknoten oder Stützstellen - sowie k zugehörige Werte <em>y</em><sub>1</sub>, <em>y</em><sub>2</sub>, ..., <em>y</em><sub>k</sub> {[Element]} <em>R</em> zugrunde. Die Stützstellen können entweder fest vorgegeben oder wählbar sein. Fallweise kann auch noch ergänzende Information vorliegen, aus der zusätzliche Forderungen an die Interpolationsfunktion abgeleitet werden, z.B. Monotinie, Konverxität, spezielles asymptotisches Verhalten etc.

Als Approximationskriterium dient bei der Interpolation die exakte Übereinstimmung der diskretisierten Modellfunktion 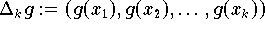mit dem Datenvektor .

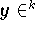dist

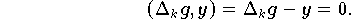
Anwendungsbeispiele

Bei vielen numerischen Verfahren werden nicht-elementare Funktionen (vgl. Elementare Funktionen als Modelle ), die nicht durch endlich viele Parameter charakterisierbar sind, zunächst durch Interpolation - meist Polynominterpolation - auf Funktionen aus endlichdimensionalen Räumen abgebildet; erst auf diese Approximationsfunktion wird dann der gewünschte Operator (zur Auswertung, Differentiation, Integration etc.) angewendet.

In der Signalverarbeitung wird das diskrtisierte (abgetastete und quantisierte) Signal oft zunächst interpoliert - vor allem durch trigonometrische Interpolation -, bevor es durch Filtermethoden verarbeitet wird (z.B. werden bei einer Tiefpaßfilterung die hochfrequenten Anteile gedämpft oder weggelassen; Tschebyscheff-Interpolation und anschließendes Weglassen der "höchsten" Terme entspricht auch einem speziellen Tiefpaßfilter).

Für die schnelle Funktionsberechnung, wie sie z.B. für Echtzeitprobleme von großer Bedeutung ist, kommt auch gelegentlich die "alte" Tabellen-Interpolation wieder zu Ehren, da eine Quick-and-Dirty Berechnung von Funktionswerten aus Tabellen manchmal schneller ist und einigen modernen Rechnerarchitekturen, wie z.B. systolischen Arrays ( [McKeown] ), eher entgegenkommt als die Auswertung von Funktionsunterprogrammen, mit denen andererseits wesetlich höhere Approximationsgenauigkeiten erreicht werden können.

Interpolationsproblem

Jede Interpolationsaufgabe besteht im allgemeinen aus drei Teilaufgaben:

  1. Eine geeignete Funktionenklasse ist zu wählen.
  2. Die Parameter eines passenden Repräsentanten aus dieser Funktionenmenge sind zu ermitteln.
  3. An der gefundenen Interpolationsfunktion sind die gewünschten Operationen (Auswertungen etc.) auszuführen.

Die Eigenschaften (Kondition etc.) und der algorithmische Aufwand müssen für die zwei rechnerischen Teilaufgaben der Interpolation - Parameterbestimmung und Manipulation (Auswertung) - getrennt untersucht werden.

Der Aufwand für die Parameterbestimmung hängt z.B. ganz wesentlich von der Funktionenklasse ab - insbesondere davon, ob es sich (bzgl. der Parameter) um ein lineares oder ein nichtlineares Interpolationsproblem handelt. Der Gesamtaufwand für eine Interpolationsaufgabe hängt nicht nur vor der Wahl der Funktionenklasse ab, sondern wird auch von den speziellen Erfordernissen der Problems bestimmt; von der Anzahl der benötigten Interpolationsfunktionen (und deren gegebenenfalls vorhandenen Abhängigkeiten), von Anzahl und Aufwand der durchzuführenden Operationen (z.B.: wieviele Werte einer Interpolationsfunktion werden benötigt?) etc.

Wahl einer Funktionsklasse

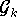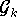Dem geplanten Verwendungzweck entsprechend ist eine geeignete Klasse ${\cal G}_k$ von Modell- bzw. Approximationsfunktionen auszuwählen. Jede Funktion g aus der Funktionenmenge ${\cal G}_k$ muß durch k Parameter festgelegt werden können:

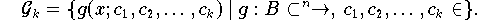
$${\cal G}_k = \lbrace g(x;c_1,c_2,\ldots,c_k) \: | \: g: B \subset \R^n \to \R, \: c_1,c_2,\dots,c_k \in \R \rbrace.$$

Die Wichtigkeit der Auswahl einer geeigneten Klasse von Modellfunktionen illustriert Abb. 6.1. Alle dort dargestellten Funktionen erfüllen das Approximationskriterium der Interpolation, das nur die Übereinstimmung an vorgegebenen Punkten fordert. Trotzdem wird nicht jede dieser Interpolationsfunktionen für jeden Anwendungszweck gleich gut geeignet sein. Erst durch die zusätzliche Forderung bestimmter Eigenschaften der Funktionen aus 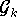${\cal G}_k$ (wie z.B. Stetigkeit, Glattheit, Monotonie, Konvexität etc.) können unerwünschte Fälle (wie z.B. Sprungstellen, Polstellen etc.) ausgeschlossen werden.

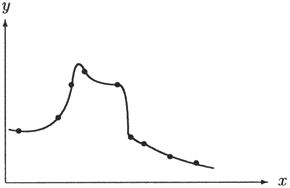
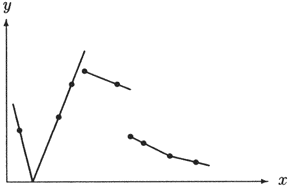
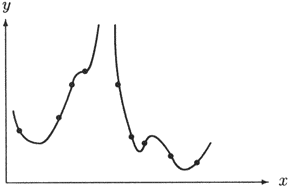
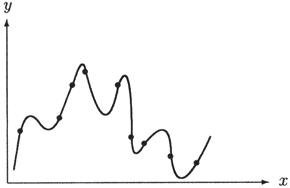
Abb. 6.1: Vier verschiedene Funktionen, die alle durch dieselben Datenpunkte ( $\bullet$ ) gehen.

Eine detaillierte Diskussion der Modellbildungsaspekte, die der Wahl einer Funktionenklasse zugrunde liegen, findet man in den Abschnitten 6.0 bis 6.5.

Bestimmung der Parameter einer Interpolationsfunktion

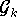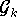Sobald eine Klasse ${\cal G}_k$ von in Frage kommenden Approximationsfunktionen festgelegt ist, muß aus ${\cal G}_k$ eine Funktion g ausgewählt werden, die an den k Stützstellen x1, x2, ..., xk die vorgegebenen Werte y1, y2, ..., yk annimmt.

Von der gesuchten Funktion g, die durch ihre Parameterwerte c1, c2, ..., ck charakterisiert wird, ist - dem Interpolationsprinzip ( siehe Abschnitt 6.3 ) entsprechend - zu fordern, daß sie durch die Datenpunkte (x1, y1), (x2, y2), ..., (xk, yk) "durchgeht"; d.h. g muß folgendes System von k Gleichungen erfüllen:

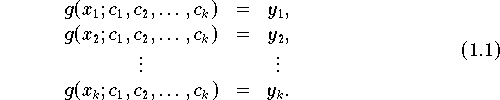
\begin{equation} \label{eqn:interpol} \begin{array}{ccc} g(x_1;c_1,c_2,\ldots,c_k) & = & y_1, \\ g(x_2;c_1,c_2,\ldots,c_k) & = & y_2, \\ \vdots & & \vdots \\ g(x_k;c_1,c_2,\ldots,c_k) & = & y_k. \end{array} \end{equation}

Gleichung 1.1

Dieses Gleichungssystem kann linear oder nichtlinear sein, je nachdem, ob g bezüglich der gesuchten Parameter c1, c2, ..., ck eine lineare oder nichtlineare Interpolationsfunktion ist (siehe Abschnitte 6.0 bis 6.5 ) .

Die Parameterbestimmung durch Lösen des Gleichungssystems (1.1) kann unter Umständen in jenen Fällen entfallen, bei denen nur Werte einer Interpolationsfunktion benötigt werden (vgl. den Neville-Algorithmus ).

Manipulation der Interpolationsfunktion

Ziel der Interpolation ist in jedem Fall die Gewinnung analytischer Daten durch Homogenisierung diskreter Daten (vgl. Analytische Modelle).

Mit den durch Interpolation gewonnenen analytischen Daten werden dann die zur Lösung des ursprünglichen Problems erforderlichen Operationen vorgenommen: Auswertung, Integrationm Diefferentiation, Nullstellenbestimmung oder andere Manipulationen.

Anmerkung Terminologie (Extrapolation)

Speziell im univariaten Fall unterscheidet man gelegentlich zwischen den Begriffen Interpolation und Extrapolation, je nachdem, ob die Auswertung der Modellfunktion im Datenintervall [ xmin, xmax] oder außerhalb des Intervalls erfolgt.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]