Schwarzinger Rainer

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Kurven

Alle bisher besprochenen mathematischen Modelle sind Funktionen im mathematischen Sinn, d.h. eindeutige Relationen. Um diese Funktionen auch zur Approximation von ebenen Kurven oder Raumkurven verwenden zu können, ist der Übergang zu einer Parameterdarstellung

$$ \Bigl( x(s),y(s) \Bigr), \quad s \in [a,b], $$

bzw.

$$ \Bigl( x(s),y(s),z(s) \Bigr), \quad s \in [a,b], $$

ein natürlicher Zugang. Im Fall der ebenen Kurven erhält man auf diese Weise zwei Approximationsprobleme des bereits besprochenen Typs:

\begin{eqnarray*} x(s), \quad s \in [a,b], \quad & \mbox{ist durch} & \quad g(s),\\ y(s), \quad s \in [a,b], \quad & \mbox{ist durch} & \quad h(s) \end{eqnarray*}

zu approximieren.

\begin{equation} \label{eqn:kurvenparam} \Bigl( g(s),h(s) \Bigr), \quad s \in [a,b] \end{equation}

ist dann die Approximationskurve. Vorsicht ist geboten, was die "optische Glattheit" der Approximationskurve betrifft: Aus der Glattheit von g und h als Funktionen von s kann nicht auf eine entsprechende Glattheit (einen gleichmäßigen Krümmungsverlauf) der ebenen Kurve bzw. Raumkurve geschlossen werden.

Beispiel: Stueckweise kubische Funktion

Eine zusätzliche Schwierigkeit gibt es bei der diskreten Approximation durch Kurven: Die den Punkten 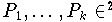$P_{1},\ldots,P_{k} \in \R^2$ zugeordneten, streng monotonen Parameterwerte

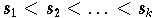
$$ s_{1} < s_{2} < \ldots < s_{k} $$

sind im allgemeinen nicht Teil der gegebenen Daten und müssen noch geeignet festgelegt werden. Erst dann kann man durch

$$ \{ (s_{1},x_{1}), (s_{2},x_{2}), \ldots, (s_{k},x_{k}) \} \qquad \mbox{und} \qquad \{ (s_{1},y_{1}), (s_{2},y_{2}), \ldots, (s_{k},y_{k}) \} $$

jeweils eine Interpolationsfunktion g(s) bzw. h(s) legen und erhält so die Kurve (1.16).


Da die Bogenlänge der natürliche Parameter einer Kurve ist, kann man z.B. durch die Definition

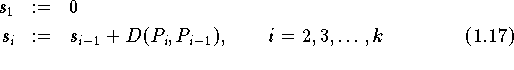
\begin{eqnarray} s_{1} & := & 0 \nonumber \\ s_{i} & := & s_{i-1} + D(P_{i},P_{i-1}), \qquad i = 2, 3, \dots, k \label{eqn:para} \end{eqnarray}

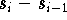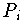eine Parametrisierung erreichen, bei der $s_{i} - s_{i-1}$ eine Approximation für die Bogenlänge zwischen $P_{i-1}$ und $P_{i}$ ist. Als Distanzfunktion D wird oft das Euklidische Abstandsmaß

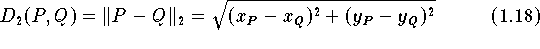
\begin{equation} \label{eqn:euklpara} D_{2}(P,Q) = \|P - Q\|_{2} = \sqrt{(x_{P} - x_{Q})^{2} + (y_{P} - y_{Q})^{2}} \end{equation}

oder ein konstanter Wert (der keiner Metrik entspricht)

\[ D(P,Q) := 1, \]

d.h. die "Einheits-Parametrisierung" mit 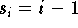$s_{i} = i-1$ , verwendet. Bei geschlossenen Kurven muß $P_1 = P_k$ gelten (siehe Abb. 1.15).


Abbildung: Parametrisierung der Punkte 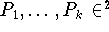$P_1,\dots,P_k \in \R^2$ für eine offene und eine geschlossene ebene Kurve. 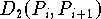$D_2(P_i,P_{i+1})$ ist die Länge der Verbindungsstrecke $\overline{P_iP_{i+1}}$ .


Eine ausführliche Diskussion der Vor- und Nachteile verschiedener Distanzfunktionen in der Parametrisierung (1.17) findet man z.B. bei [Epstein], [de Boor], und [Foley], wobei in vielen Fällen dem Euklidischen Abstandsmaß (1.18) der Vorzug gegeben wird.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]