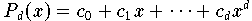 (Formel 9.28)
(Formel 9.28)Autor: Stefan Huber
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Eine der wichtigsten Manipulationen mit Interpolationspolynomen ist deren
Auswertung (die Bestimmung von Funktionswerten) an einer oder mehreren
Stellen.
Horner-Algorithmus
Für ein Polynom der Potenzform
gibt es eine bekannte Rekursion- das Horner-Schema - zur
Berechnung des Wertes von
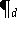 an der stelle x:
an der stelle x:
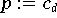
do
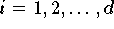
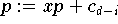 (Formel 9.29)
(Formel 9.29)
end do
Das Horner-Schema benötigt jeweils d Addidionen und Multiplikationen
zur Berechnung des gesuchten Funktionswertes
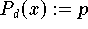 .
Dieser Rechenaufwand für die Auswertung eines Polynoms mit gegebnen
Koeffizienten bezüglich der Monombasis
.
Dieser Rechenaufwand für die Auswertung eines Polynoms mit gegebnen
Koeffizienten bezüglich der Monombasis
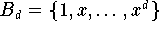 ist optimal. Es gibt kein Verfahren, das mit weniger
Rechenoperationen auskommt.
ist optimal. Es gibt kein Verfahren, das mit weniger
Rechenoperationen auskommt.
Als Vermutung stammt diese
Optimalitätsaussage aus einer Arbeit von
Ostrowski [318]
aus dem Jahre 1954, die man oft als die Geburtsstunde der
albebraischen Komplexitätstheorie
ansieht. Der Beweis der
Vermutung wurde 1966 von
Pan [320]
geliefert.
Clenshaw-Algorithmus
Erhält man als Resultat eines Interpolations- oder
Approximationsverfahrens ein Polynom in der Tschebyscheff-Form
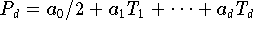 und will man dieses an der Stelle x
auswerten, dann könnte man es zuerst in die Potenzform
(9.28)
bringen und dann das Horner-Schema
(9.29)
anwenden.
und will man dieses an der Stelle x
auswerten, dann könnte man es zuerst in die Potenzform
(9.28)
bringen und dann das Horner-Schema
(9.29)
anwenden.
Die dafür erforderliche Umrechnung der Koeffizienten ist aber mit
unnötigem Aufwand verbunden und verschlechtert außerdem
die Genauigkeit des Resultats. Günstiger ist es, mit den
Koeffizienten
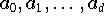 der Tschebyscheff-Entwicklung den Clenshaw-Algorthmus
anzuwenden, der als Resultat den gesuchten Funktionswert
der Tschebyscheff-Entwicklung den Clenshaw-Algorthmus
anzuwenden, der als Resultat den gesuchten Funktionswert
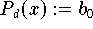 liefert:
liefert:
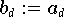
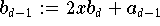
do 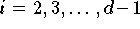
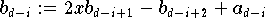
end do
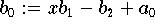
Eine genaue Herleitung des Clenshaw-Algorthmus, der auf der Rekursion (9.12) beruht, und einen Beweis seiner numerischen Stabilität findet man z.B. bei Fox und Parker [199].
Software (Auswertung eines Polynoms in Tschebyscheff-Darstellung
Ein Polynom, das durch Koeffizienten seiner Tschebyscheff-Darstellung
gegeben ist, kiann mittels der Unterprogramme NAG/e02aef bzw. NAG/e02akf
an einer gegebenen Stelle ausgewertet werden, NAG/e02akf läßt
sich dabei flexibler verwenden als NAG/e02aef, besitzt aber auch eine
entsprechend komplizierte Parameterliste.
Auch wenn man an Ableitungswerten oder Integralen
interessiert ist, gibt es Algorithmen und Programme, die auf speziell für Ableitungen oder Integrale modifizierten Koeffizienten der Tschebyscheff-Darstellung des Interpolationspolynoms beruhen.
Software (Differenzieren und Integrieren von Polynomen in
Tschebyscheff-Darstellung)
Die Tschebyscheff-Darstellung der ersten Ableitung eines bereits in
Tschebyscheff-Darstellung gegebenen Polynoms berechnet das Unterprogramm
NAG/e02ahf. Die Koeffizienten der Tschebyscheff-Darstellung des
unbestimmten Integrals für ein solches Polynom können mit
Hilfe von NAG/e02ajf ermittelt werden.
Algorithmus von de Casteljau
Ein Polynom, das durch die Koeffizienten
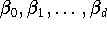 seiner
Bézier-Darstellung (9.11)
gegeben ist, läßt sich mit der Rekursion
seiner
Bézier-Darstellung (9.11)
gegeben ist, läßt sich mit der Rekursion
do 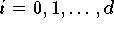
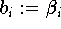
end do
do 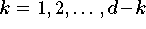
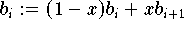
end do
auswerten, die als Resultat
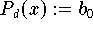 liefert (
Locher [62]).
liefert (
Locher [62]).
Wenn man nur einen Wert (oder eine geringe Anzahl von Werten)
des Interpolationspolynoms benötigt, dann wäre es
unzweckmäßig, zuerst die Koeffizienten einer der obigen
Darstellungen des Interpolationspolynoms zu berechnen und dieses dann
an der gewünschten Stelle auszuwerten.
Für diese Problemstellung gibt es spezielle Algorithmen, die
bezüglich des Rechenaufwandes günstiger sind. Diese
Verfahren beruhen auf dem Prinzip der sukzessiven linearen
Interpolation, deren Grundlage folgender Satz ist:
Satz 9.3.2 (Lemma von Aitken) so erhält man das Interpolationspolynom
Beweis:
An der Knotenmenge
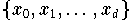 seien die Werte
seien die Werte
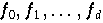 vorgegeben. Hat man für
vorgegeben. Hat man für
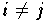
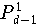 zu den Knoten
zu den Knoten
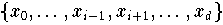 ,
,
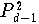 zu den Knoten
zu den Knoten
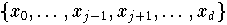 ,
,
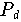 zu der gesamten Knotenmenge durch folgende Linearkombinationen:
zu der gesamten Knotenmenge durch folgende Linearkombinationen:
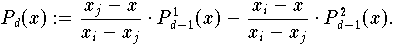
Ausgehend vom Lemma von Aitken kann man eine Vielfalt von iteraktiven
Interpolationsverfahren konstruieren, die sich hauptsächlich in
der Reihenfolge der Verwendung der Wertepaare
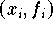 unterscheiden. Die verbreitetsten Verfahren sind jene von Neville
und von Aitken. Im folgenden soll die iterierte Interpolation nach
E.H. Neville - das
Neville-Schema
- beschrieben werden. Dabei
wird das Lemma von Aitken sukzessive auf die Polynome
unterscheiden. Die verbreitetsten Verfahren sind jene von Neville
und von Aitken. Im folgenden soll die iterierte Interpolation nach
E.H. Neville - das
Neville-Schema
- beschrieben werden. Dabei
wird das Lemma von Aitken sukzessive auf die Polynome
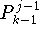 zu den Knoten
zu den Knoten 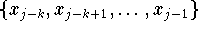 sowie
sowie 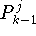 zu den Knoten
zu den Knoten 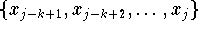 angewendet; das resultierende Polynom
angewendet; das resultierende Polynom
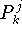 interpoliert dann an den Knoten
interpoliert dann an den Knoten
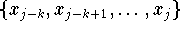 :
:
do 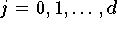
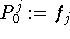
end do
do 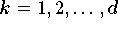
do 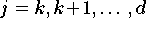
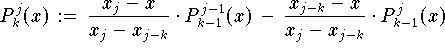 (Formel 9.30)
(Formel 9.30)
end do
end do
Um diese Rekursion zur Berechnung des Wertes von
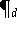 an einer konkreten Stelle
an einer konkreten Stelle
 zu verwenden, muß man lediglich im Neville-Schema
(9.30)
x durch
zu verwenden, muß man lediglich im Neville-Schema
(9.30)
x durch
 ersetzen;
ersetzen; 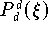 ist dann das gesuchte Resultat.
ist dann das gesuchte Resultat.
Software (Direkte Interpolation einzelner Funktionswerte)
Wird für eine Menge gegebener Datenpunkte keine expliziete
Darstellung des interpolierenden Polynoms benötigt, sondern nur
ein einzelner Wert dieser Funktion, so kann dieser mit dem
Unterprogramm NAG/e01aaf nach dem Aitken-Verfahren durch
sukzessive lineare Interpolation berechnet werden. Die Datenpunkte
können dabei beliebig verteilt sein. Dabei wird nicht nur das
Endresultat
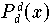 ,
sondern auch alle Resultate
,
sondern auch alle Resultate
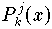 von Teilinterpolationen zurückgeliefert. Duch Vergleich dieser
Werte kann man sich Informationen über die vermutliche
Größe des absoluten Interpolationsvehlers
von Teilinterpolationen zurückgeliefert. Duch Vergleich dieser
Werte kann man sich Informationen über die vermutliche
Größe des absoluten Interpolationsvehlers
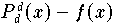 verschaffen.
verschaffen.
Soferne äquidistante (gleichabständige) Datenpunkte gegeben
sind, kann man das Unterprogramm NAG/e01abf verwenden. Dieses
berechnet einen einzelnen Wert des Interpolationspolynoms mit Hilfe
der Everett-Formel (
Hildebrand [55]).
Autor: Stefan Huber
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]