[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

9.5 Stationäre Iterative Verfahren

Im Vorherigen Kapitel wurden iterative Methoden zur Lösung linearer Gleichungssysteme als Minimierungsverfahren für quadratische Funktionen hergeleitet.

Für allgemeine (nichtsymmetrische und/oder nicht-definite) Matrizen sind iterative Verfahren mittels Methoden für nichtlineare Gleichungssysteme besser geeignet. Hier nochmals die Funktionsweise kurz zusammengefaßt. Weiters eine Aufzählung der Verfahren, die stationäre iterative Lösungsmethoden verwenden.

- Definition: Stationäre Iteration
- Jacobi-Verfahren
- Gauss-Seidel-Verfahren
- SOR-Verfahren
- SSOR-Verfahren

Für die iterative Lösung allgemeiner (nichtsymetrischer und/oder nicht-definiter) Matrizen können Minimierungsverfahren nicht angewandt werden. Eine Möglichkeit dieses Gleichungssystem zu lösen bieten die stationären iterativen Verfahren.

Um ein Gleichungssystem iterativ zu lösen, das in Fixpunktform

x = T(x)

gegeben ist, wählt man einen Startvektor \[x^{(0)}\in \mathbb R^{n}\] und setzt die jeweils letzte Näherung in T(.) ein:

\[x^{(k)}:=T(x^{(k-1)}),\hspace {2cmk=1,2,3,...}\]

9.5.1 Definition: Stationäre Iteration

Eine Iteration 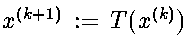\( x^{(k+1)}:=T(x^{(k)}) \) nennt man stationär, wenn die Iterationsvorschrift T unabhängig vom aktuellen Iterationsschritt definiert ist.

Die Grundform stationärer Iterationsverfahren zur Lösung linearer Gleichungssysteme ist von der Bauart:
\[x^{(k)}:=Bx^{(k-1)}+c,\hspace {2cmk=1,2,3,...}\]
wobei \[B\in \mathbb R^{n\times n}\] und \[c\in \mathbb R^{n}\] von k unabhängig sind. Um ein lineares Gleichungssystem Ax = b in eine iterierfähige Form zu bringen, kann man z. B. die Koeffizientenmatrix additiv in

A = L + D + U

aufspalten. Die Summanden sind \[D=diag(a_{11},...,a_{nm)}\] , die strikte untere Dreiecksmatrix L und ihr "Gegenstück" U:

\[L:=\left( \begin{array}{ccccc} 0 & 0 & \cdots & 0 & 0\\ a_{21} & 0 & \cdots & 0 & 0\\ a_{31} & a_{32} & \cdots & 0 & 0\\ \vdots & \vdots & & \vdots & \vdots \\ a_{n-1,1} & a_{n-1,2} & \cdots & 0 & 0\\ a_{n1} & a_{n2} & \cdots & a_{m,n-1} & 0 \end{array} \right) ,\: \: U:=\left( \begin{array}{cccc} 0 & a_{12} & \cdots & a_{1n}\\ 0 & 0 & \cdots & a_{2n}\\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & a_{n-2,n}\\ 0 & 0 & \cdots & a_{n-1,n}\\ 0 & 0 & \cdots & 0 \end{array} \right) .\]

Das Ausgangssystem läßt sich mit dieser Zerlegung als

Dx = b - Lx - Ux

schreiben. Wenn A nichtsingulär ist, läßt sich dies nach eventuellem Zeilen und/oder Spaltenvertauschen auf jeden Fall erreichen. Man kann also obige Gleichung anschreiben als

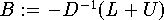\[x=D^{-1}b-D^{-1}(L+U)x.\]

Mit \[B:=-D^{-1}(L+U) und \[c:=D^{-1}b\] erhält man daraus die Fixpunktform

\[x=T(x):=Bx+c\]

Das entsprechnede stationäre Iterationsverfahren ist das Jacobi-Verfahren

Zu den stationären iterativen Lösungsmethoden linearer Gleichungssysteme zählen die nun folgende Verfahren:

Jacobi-Verfahren

Ein einzelner Iterationsschritt dieses Verfahrens entspricht der lokalen Lösung für eine Variable (vergl. dazu das vorherigen Kapitel ). Sie ist leicht implementierbar, konvergiert meist aber sehr langsam.

Gauß-Seidel-Verfahren

In diesem Verfahren werden die erhaltenen Näherungswerte sofort für die weitere Berechnung weiterverwendet. Dadurch erhöht sich die Konvergenzgeschwindigkeit, ist aber noch immer relativ gering. Näheres dazu im Kapitel über das Jacobi-Verfahren

SOR-Verfahren

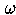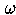Diese sind aus dem Gauß-Seidel-Verfahren unter Verwendung eines Extrapolationsfaktors $\omega$ abgeleitet. Bei guter Wahl von $\omega$ kann eine sehr schnelle Konvergenz erreicht werden.

SSOR-Verfahren

Die symmetrischen SOR-Verfahren erreichen gegenüber den SOR-Verfahren oft keine Effizienzsteigerung. Sie werden jedoch zur Vorkonditionierung nichtstationärer Methoden eingesetzt.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]