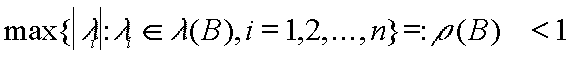[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

9.5.2 Gauß-Seidel-Verfahren

diese Seite ist noch in Arbeit

Worum geht's?

Das Gauß-Seidel-Verfahren ist eine stationäre iterative Lösungsmethode linearer Gleichungssysteme. Es ist dem Jacobi-Verfahren sehr ähnlich. Es gelten die gleichen mathematischen Voraussetzungen:

Mathematische Voraussetzungen

Das Gleichungssystem Ax=b muß in Fixpunktform x=T(x) gegeben sein. Die Diagonalmatrix muß nichtsigulär sein, d.h. alle Werte in D müssen von Null verschieden sein. Die Kontraktivität vonT(x):=Bx+c (T(.) ist Iterationsvorschrift, B ist Iterationsmatrix) mußgegeben sein, um das System lösen zu können. Eine notwendige und hinreichende Bedingung dafür ist:

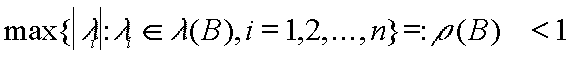$$\rho(B):=\max\{|\lambda_i|:\lambda_i\in\lambda(B),\,i=1,2,\dots,n\}$$(Spektralradius kleiner 1)

Gauß-Seidel-Verfahren

Annahme: alle x-Werte (bisauf den zu berechnenden i-ten) sind schon bekannt.

Löst man die i-te Gleichung des Systems Ax=b nach der i-ten Komponente von x auf, so erhält man

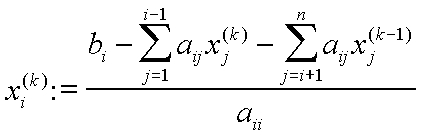
x_{i}^{(k)}:=(b_{i}-\sum_{j=1}^{i-1}a_{ij}x_{j}^{(k)}-\sum_{j=i+1}^{n}a_{ij}x_{j}^{(k-1)})/a_{ii}

Das k gibt den Iterationsschritt an.

Zur Berechnung der k-ten Annäherung der i-ten Variablen verwendetman die (in diesem k-ten Iterationsschritt schon berechneten) x-Werte

x1..xi-1

und die im letzten Iterationsschritt (k-1) berechneten x-werte

x1+1..xn

Der Algorithmus für das Gauß-Seidel-Verfahren:

do k=1,2,3,....

    do i = 1,2,...,n

\[Ax=b\]

    end do

    if Abbruchkriterium erfüllt then exit

enddo

Die einzelnen Gleichungen des Systems Ax= b kann man auch geordnet auflösen, wobei man bereits berechnete Werte sofort im nächsten Rechenschritt verwendet. In diesem Fall müssen alle Berechnungen seriell ausgeführt werden, da jede Komponente der neuen Iteration von allen zuvor berechneten Komponenten abhängt. Der Vektor X (k) ist von der Reihenfolge der Gleichungsauflösungen abhängig;bei der Änderung der Reihenfolge ergeben sich andere Werte der Komponenten, weshalb das Verfahren auch den Namen Einzelschrittverfahren trägt. Ist A eine schwachbesetzte Matrix, so ist es möglich, daß die vielen Nullen den Einfluß vorhergehender Komponenten bei der Berechnung bestimmter Komponenten (-gruppen ) verschwinden lassen. Durch geschickte Auswahl der Reihenfolge ist es dann möglich, einige Aktualisierungen parallel durchzuführen, was im Idealfall weit höhere Konvergenzgeschwindigkeit bringt. Allerdings kann eine ungünstige Auswahl die Konvergenz auch stark verschlechtern. Das Abbruchkriterium prüft z.B. ob die gewünschte Genauigkeit (schon) erreicht ist.

Konvergenzverhalten

Durch die Verwendung der jeweils aktuellsten Näherungswerte sollte man annehmen, daß das Gauß Seidel Verfahren rascher konvergiert als das Jacobi-Verfahren . In Spezialfällen trifft diese Vermutung auch zu: ist A eine reguläre, strickt diagonaldominante Matrix, so konvergiert das Gauß Seidel Verfahren für jeden Startvektor X (0) . Die Konvergenzgeschwindigkeit ist dabei größer oder zumindest gleich groß wie beim Jacobi-Verfahren . Unter noch stärkeren Einschränkungen der Klasse der Matrizen des linearen Gleichungssystems gilt sogar, daß das Einzelschrittverfahren doppelt so rasch konvergiert wie das Gesamtschrittverfahren ( Jacobi-Verfahren ). Die schnellere Konvergenz des Einzelschrittverfahrens läßt sich nicht generell beobachten. Es gibt sogar Fälle, bei denen das Gauß Seidel Verfahren divergiert, obwohl das Jacobi-Verfahren konvergiert. Konvergenz kann aber für die in der Praxis häufig auftretenden symmetrischen und positiv definieten Matrizen garantiert werden: ist A eine symmetrische und positiv definite Matriz, so konvergiert das Gauß Seidel Verfahren für jeden Startvektor X (k) .

Anwendung des Gauß-Seidel-Verfahrens

Bei jedem Gleichungssystem ist es wichtig, so schnell wie möglich zur (befriedigenden) Lösung zu kommen. Bei iterativen Verfahren ist die Konvergenzgeschwindigkeit (also die Anzahl der erforderlichen Iterationsschritte) ausschlaggebend für die Effizienz des Verfahrens. Die Anwendung des Gauß-Seidel-Verfahrens anstatt des Jacobi-Verfahren rentiert sich (eventuell) bei regulärer, strikt diagonaldominanter Matrix A des Gleichungssystems. Bei symmetrischer, positiv definiter Matrix (tritt in der Praxis häufig auf) konvergiert das Gauß-Seidel-Verfahren auf jeden Fall.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]