[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

9.4.3 Gesamtschritt- (Jacobi-) Verfahren

Kleine Einführung in die Materie

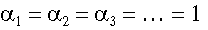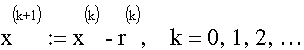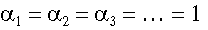
Dieses Verfahren wird ebenfalls zur iterativen Lösung eines linearen Gleichungssytems verwendet.
Die Konvergenz ist für dieses Verfahren besonders wichtig, da man bei jedem Iterationsschritt bessere Näherungen haben möchte, als die vorherigen Komponenten es waren.
Wenn für eine Matrix A das Zeilensummen-Kriterium erfüllt oder A positiv definit ist, dann konvergiert dieses Verfahren für einen beliebigen Startvektor gegen die gesuchte Lösung von Ax=b.
Das Zeilensummen-Kriterium ist eine Ungleichung, die besagt, daß in jeder Zeile der Matrix A das Diagonalelement dem Betrage nach größer als die Summe der Nicht-Diagonalelemente ist.
Die numerische Berechnung verläuft in einem Iterationsschritt komponentenweise. Im Gauß-Seidl-Verfahren hingegen, werden schon die neu berechneten Komponenten in den Iterationsschritt hineingenommen.

Mathematische Theorie

Nimmt man den Gradienten -r^(k) als Iterationsrichtung, wählt aber konstant

$\alpha_1 = \alpha_2 = \alpha_3 = \cdots = 1$
geht also nicht zum Minimalpunkt von f, so erhält man die als Gesamtschritt- oder Jacobi- Verfahren bezeichnete Methode

$\xke := \xk-r^{(k)},\quad k=0,1,2,\dots$
bei der man jede Komponente x_i^(k) so verändert, daß das Residuum der i-ten Gleichung Null wird. Die Änderungen -r₁^(k), -r₂^(k), ..., -r_n^(k) werden alle gemeinsam zur Korrektur verwendet, woraus sich die Bezeichnung Gesammtschrittverfahren ableitet.
Die problemunabhängige konstante Schrittweitenwahl ist die Ursache für das schlechtere Konvergenzverhalten des Gesamtschrittverfahrens im Vergleich zum Einzelschritt-Verfahren.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]