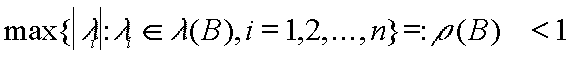(Spektralradius kleiner 1)
Das Jacobi-Verfahren ist eine stationäre iterative Lösungsmethode linearer Gleichungssysteme. Bei diesem Verfahrenentspricht ein Iterationsschritt der lokalen Lösung für einerVariablen. Das Verfahren ist ein Näherungsverfahren, bei dem man vorhersagen kann, nach wievielen Iterationsschritten der (maximal) erlaubte Fehler unterschritten wird.
Das Gleichungssystem Ax=b muß in Fixpunktform x=T(x) gegeben sein. Die Diagonalmatrix muß nichtsigulär sein, d.h. alle Werte in D müssen von Null verschieden sein. Die Kontraktivität vonT(x):=Bx+c (T(.) ist Iterationsvorschrift, B ist Iterationsmatrix) mußgegeben sein, um das System lösen zu können. Eine notwendige und hinreichende Bedingung dafür ist:
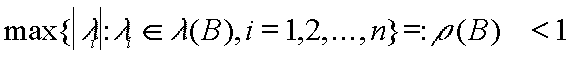(Spektralradius kleiner 1)
Gegeben: ein Gleichungssystem Ax=b in Fixpunktform .
Annahme: alle x-Werte (bisauf den zu berechnenden i-ten) sind schon bekannt.
Löst man die i-te Gleichung des Systems Ax=b nach der i-ten Komponente von x auf, so erhält man
![\[x_{i}^{(k)}=(b_{i}-\sum_{j\ne i} a_{ij}x_{j}^{(k-1)})/a_{ii}\]](pic/i05_0102.gif)
Das k gibt den Iterationsschritt an. Zur Berechnung der k-ten Annäherung verwendetman die x-Werte der (k-1)-ten Annäherung.
Der Algorithmusfür das Jacobi-Verfahren:
do k=1,2,3,....
do forall i in [1..n]
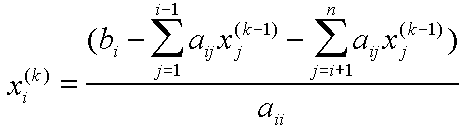
end do
if Abbruchkriterium erfüllt then exit
enddo
Es gibt einen Startvektor für alle x-Werte. DieserStartvektor enthält beliebige Werte.
Beim ersten Iterationsschritt werden die x-Werte des Startvektors verwendet, um daraus neue x-Werte zu berechnen. Bei der zweiten Iterationwerden zur Berechnung bereits die Werte verwendet, die bei derersten Iteration berechnet wurden, usw.
Da keine Werte verwendet werden, die im aktuellen Iterationsschritt berechnet wurden, können alle Berechnungen in der FORALL-Schleife sogar gleichzeitig durchgeführt werden.
Deshalb heißt dasJacobi-Verfahren auch Gesamtschrittverfahren.
Das Abbruchkriterium prüft z.B. ob die gewünschte Genauigkeit (schon) erreicht ist.
Bei der Abbildung T(x) := Bx + c ist wegen
||T(x)-T(y)||=||Bx-By||=||B(x-y)||<=||B|| ||x-y||
die Lipschitz-Konstante von T durch L="||B||" gegeben. Deshalb ist die Abbildung T(x) genau dann kontrahierend, wenn es eine Matrixnorm ||.|| gibt, für die ||B||<1 gilt.
Ist die Systemmatrix A strikt diagonaldominant, so erfüllt die Zeilensummennorm der Iterationsmatrix B="(L+U)/(-D)" das Konvergenzkriterium ||B||<1.
[strikt diagonaldominant hei"st: der Betrag des Diagonalelements einer Spalte ist grö"ser als die Summe der Beträge aller restlichen Spaltenelemente.]
Da es immer (für jedes Epsilon>0)eine Matrixnorm ||.||gibt, bei der ||B|| <= (Spektralradius von B) + Epsilon gilt, sind Spektralradius und Matrixnorm sehr eng verbunden.
Die Konvergenzgeschwindigkeit eines stationären iterativen Verfahrens wird sehr stark durch den Spektralradius von B bzw. ||B|| beeinflußt.
Um eine Genauigkeit
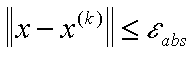
zu erreichen, sind
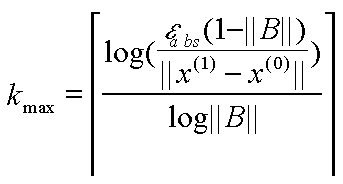
Iterationsschritte erforderlich. D.h. je stärker die Diagonalelemente der Matrix A die Nicht-Diagonal-Elemente dominieren, desto rascher ist die Konvergenz (weil ||B|| umso kleiner ist).
Bei jedem Gleichungssystem ist es wichtig, so schnell wie möglich zur (befriedigenden) Lösung zu kommen. Bei iterativen Verfahren ist die Konvergenzgeschwindigkeit (also die Anzahl der erforderlichen Iterationsschritte) ausschlaggebendfür die Effizienz des Verfahrens. Die Anwendung desJacobi-Verfahrens rentiert sich bei vollbesetzter Matrix A nurdann, wenn gilt:
erforderliche Iterationsschritte kleiner n/3
(bei symmetrischer Matrix sogar kleiner n/6).
Bei den meisten praktisch auftretenden Problemen ist dies nicht gegeben. ergo: Vor Implementierung und Anwendung des Jacobi-Verfahrens prüfen, ob es überhaupt der Mühe wert ist.