[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

9.4.1 Einzelschritt- (Gauß-Seidl-) Verfahren

Kleine Einführung in die Materie

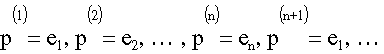
Das Gauß-Seidl-Verfahren wird zur iterativen Lösung von linearen Gleichungssytemen verwendet.
Die Konvergenz ist für dieses Verfahren besonders wichtig, da man bei jedem Iterationsschritt bessere Näherungen haben möchte, als die vorherigen Komponenten es waren.
Wenn für eine Matrix A das Zeilensummen-Kriterium erfüllt oder A positiv definit ist, dann konvergiert dieses Verfahren für einen beliebigen Startvektor gegen die gesuchte Lösung von Ax=b.
Das Zeilensummen-Kriterium ist eine Ungleichung, die besagt, daß in jeder Zeile der Matrix A das Diagonalelement dem Betrage nach größer als die Summe der Nicht-Diagonalelemente ist.
Im Gegensatz zum Gesamtschritt-Verfahren verwendet man beim Gauß-Seidl-Verfahren die neu berechneten Komponenten.

Mathematische Theorie

Wählt man als Richtungen für die Minimierung (ohne Rücksicht auf die Residuen zu nehmen) zyklisch die Koordinatenrichtungen

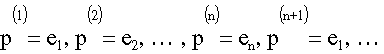
p^{(1)} = e_1,\,\,p^{(2)}=e_2,\,\dots\,,p^{(n)}=e_n,\,\,p^{(n+1)}=e_1,\,\dots

so erhält man
\alpha_{m+1} & := & -\frac{\langle r^{(m)},p^{(m+1)}\rangle}{\langle Ap^{(m+1)}, p^{(m+1)}\rangle} = -\frac{\langle r^{(m)},e_i\rangle}{\langle Ae_i,e_i\rangle}= -\frac{r_i^{(m)}}{a_{ii}}\nonumber\\[1ex]

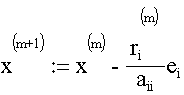x^{(m+1)}& := & x^{(m)}-\frac{r_i^{(m)}}{a_{ii}}e_i\qquad\mbox{mit}\quad i:=m\,({\rm mod}\, n)\,+\,1 mit i := m (mod n) + 1

Im Minimierungsschritt wird nur die i-te Komponente des Vektors x(m) verändert:

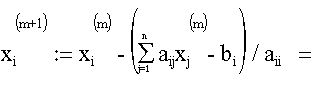
x_i^{(m+1)} & := & x_i^{(m)}-(\sum_{j=1}^n a_{ij}x_j^{(m)}-b_i)/a_{ii}=

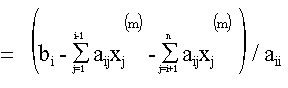
& = & (b_i-\sum_{j=1}^{i-1}a_{ij}x_j^{(m)}-\sum_{j=i+1}^n a_{ij}x_j^{(m)})/a_{ii}

Faßt man die n Komponenten, die das Resultat eines Zyklus sind, in einem Vektor x(k) zusammen, so erhält man die Methode, die Einzelschritt- oder Gauß-Seidel-Verfahren genannt wird.
Die Abnahme von f beim Minimierungsschritt ist durch folgendes gegeben:

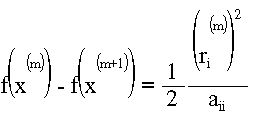
f(x^{(m)})-f(x^{(m+1)})=\frac{1}{2}\,\frac{\left(r_i^{(m)}\right)^2}{a_{ii}}

Die Folge {f(x(m))} ist daher monoton fallend und nach unten beschränkt (weil f ein endliches Minimum besitzt), also konvergent.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]