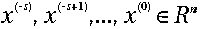
ausgegangen - ähnlich wie beim Lösen nichtlinearer Gleichungen im Kapitel 14.
Bei diesen Lösungsverfahren für lineare Gleichungen wird von
einem oder meheren Startwerten
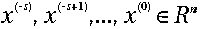
ausgegangen - ähnlich wie beim Lösen nichtlinearer Gleichungen im
Kapitel 14.
Wir definieren eine Folge, {x(k) : k=1,2,3,...},
deren Elemente möglichst gegen unseren Lösungsvektor
x* der Gleichung
Ax = b konvergieren sollen.
Die Folge {x(k)} sieht im allgemeinen dann so aus:
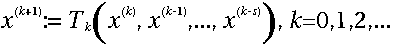
Wichtige Spezialfälle von 16.11 sind die (in)stationären Einschrittverfahren:
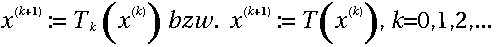
Durch diese zwei Definitionen entsteht eine unendliche Folge.
Wir möchten nun basierend auf einer Iterationsvorschrift Tk
einen Algorithmus zur Lösung linearer Gleichungssysteme
definieren.
Dabei müssen wir die unendliche Folge {x(k)}
allerdings nach endlich vielen Schritten abbrechen, um zu einem Ergebnis
zu kommen.
Dadurch tritt aber natürlich ein Verfahrensfehler auf,
da die Berechnung ja abgebrochen wird.
Diesen nennt man dann bezeichnenderweise
Zum Beispiel wenn dieser Fehler durch die Diskretisierung partieller
Differentialgleichungen entstanden ist, hat man sowohl auf der linken Seite
mit der Matrix A als auch auf der rechten Seite mit b keine
genauen Werte mehr.
Hier wäre es eher sinnlos, eine Lösung von Ax = b
zu berechnen, die viel genauer
ist als die fehlerbehaftete Differentialgleichung.
Das Lösungsverfahren muß also zu einem geeigneten Zeitpunkt
abgebrochen werden. Dieser Zeitpunkt richtet sich nach dem Problem - generell
sollte ein gutes Abbruchkriterium:
do k=1,2,3,...
Berechnung von
Berechnung von
Berechnung von
if k > = maxif or
|| r (k) || < = stop_tol . (norm_A . || x (k) || + norm_b) then exit
end do
Die Größen maxit, norm_A, norm_B und stop.tol legt man dabei so fest:
| Bezeichnung | Wertebereich | Erklärung |
|---|---|---|
| maxit | natürliche Zahl | maximale Anzahl an Iterationsschritten |
norm_A
| reelle Zahl |
Näherungswert für || A ||
(Oft reicht hier der Absolutwert des größten Matrixelements aus.)
|
|
| norm_b | reelle Zahl | Näherungswert für || B || (Auch hier reicht eine Approximation wie für norm_A aus). |
| stop_tol | reelle Zahl | Maßzahl für die geforderte Größe (eigtl. "Kleinheit")
des Residuums r(k) := Ax(k) - b. Man könnte zum Beispiel stop_tol entsprechend dem relativen Datenfehler von A und b wählen: Im Falle eines Datenfehlers bei A in der Größenordnung ±10-4 sollte man 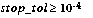 wählen, da weitere Iterationen keine Genauigkeitsverbesserung mehr
bringen würden.
wählen, da weitere Iterationen keine Genauigkeitsverbesserung mehr
bringen würden.Allgemein sollte immer gelten: eps < stop_tol < 1. |
Hinweis: Bei sehr geringer Veränderung der x(k)
(also in der Nähe der Lösung) muß || x(k) ||
nicht jedesmal neu berechnet werden.
Ist || A || gerade nicht griffbereit, kann man die
Bedingung an die Residuumsnorm (siehe Algorithmus
unter "|| r(k) || ")
auf  ändern.
ändern.
Die Fehlergrenze ergibt sich immer zu
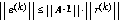 .
.