[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

9.4.2 Gradientenverfahren

Kleine Einführung in die Materie

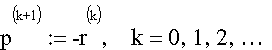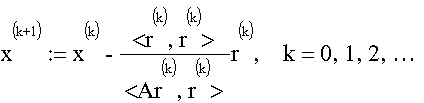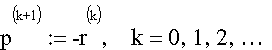
Dieser Algorithmus wird ebenfalls zur iterativen Lösung eines linearen Gleichungssystems verwendet.
Hier ist jedoch zu beachten, daß der Richtungsvektor p, der im Minimierungsschritt verarbeitet wird, nicht orthogonal zum Residuenvektor r⁽⁰⁾ gewält werden darf. Andernfalls ergibt sich x⁽¹⁾ = x⁽⁰⁾.

Mathematische Theorie

Das allgemeine Minimierungsprinzip läßt noch die Wahl der Richtungsvektoren p⁽¹⁾, p⁽²⁾,p⁽³⁾, ... frei, wobei nur Richtungen p^(k+1) orthogonal zum Residuum r^(k) zu vermeiden sind.
Der Residuenvektor r^(k) als Gradient der zu minimierenden quadratischen Funktion f gibt an der Stelle x^(k) jene Richtung an, in welcher f lokal am stärksten zunimmt. Es ist daher naheliegend, als Minimierungsrichtungen

$p^{(k+1)}:=-r^{(k)},\quad k=0,1,2,\dots$
zu definieren, also jeweils die Richtung des (lokal) stärksten Abstiegs zu verwenden:

$\xke:=\xk-\frac{\langle r^{(k)},r^{(k)}\rangle}{\langle Ar^{(k)},r^{(k)} \rangle}r^{(k)},\quad k=0,1,2,\dots$
In der Praxis zeigt sich, daß trotz der lokal besten Minimierungsrichtung (mit der größtmöglichen Verkleinerung von f) das Konvergenzverhalten der Methode des steilsten Abstiegs nicht gut ist. Man benötigt oft sehr viele Iterationsschritte, um in die Nähe der Lösung x^* zu kommen.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]