[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Bei Interpolationsproblemen müssen zwei unterschiedliche Konditionsbegriffe auseinandergehalten werden:
| die Kondition der Funktionswerte | |
| und | die Kondition der Koeffizienten . |
Unter der Kondition der Funktionswerte versteht man die Empfindlichkeit der Werte Pd(x) des Interpolationspolynoms gegenüber Störungen der Daten, also jener Funktionswerte, die das Polynom Pd definieren. Diese Kondition ist - im Gegensatz zur Kondition der Koeffizienten - unabhängig von der verwendeten Basis (z.B. Lagrange-, Bernstein- oder Tschebyscheff-Basis). Man untersucht in diesem Fall, wie sich der Übergang von den
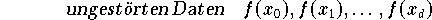
zu den
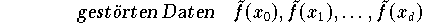
in einer Änderung von
![\[
P_d(x) = \sum_{i=0}^df(x_i) \phi_{d,i}(x) \qquad \mbox{zu} \qquad
\tilde{P}_d(x) = \sum_{i=0}^d\tilde{f}(x_i) \phi_{d,i}(x)
\]](pic/f07_0802.gif)
auswirkt.
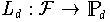
ist jene "Vorschrift", die einer Funktion
 das Interpolationspolynom zu bestimmten Knoten
das Interpolationspolynom zu bestimmten Knoten
 zuordnet:
zuordnet:
![\[
L_d f = \sum_{i=0}^d f(x_{d,i})\phi_{d,i}(x).
\]](pic/f07_0806.gif)
Da es sich bei
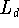 um einen linearen Operator handelt, ist wegen
um einen linearen Operator handelt, ist wegen
![\[
\|L_d f - L_d \tilde{f}\| \le
\|L_d\| \cdot \|f - \tilde{f}\|
\]](pic/f07_0808.gif)
dessen (absolute) Kondition durch
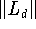 charakterisierbar.
Die Konditionszahl
charakterisierbar.
Die Konditionszahl
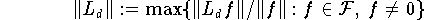
läßt sich durch die Lebesgue-Konstante abschätzen. Aus
![\begin{eqnarray*}
\|L_df\|_{\infty} & =
& \max_{x \in [a,b]}|\sum_{i=0}^d
f(x_{d,i})\phi_{d,i}(x)| \le \\
& \le & \max_{x \in [a,b]}
\sum_{i=0}^d
|f(x_{d,i})| |\phi_{d,i}(x)| \le \\
& \le & \max_{x \in [a,b]} |f(x)|
\max_{x \in [a,b]} \sum_{i=0}^d
|\phi_{d,i}(x)| ~ = ~
\|f\|_{\infty} \Lambda_d(K)
\end{eqnarray*}](pic/f07_0811.gif)
folgt nämlich
![\[
\|L_d\|_{\infty} \,=\, \max \{ \|L_df\|_\infty / \|f\|_\infty: f \in
{\cal F}\setminus\{0\}\,\} \,\le\, \Lambda_d(K).
\]](pic/f07_0812.gif)
Tabelle
Lebesgue-Konstanten
und Abb.
Lebesgue-Konstanten
enthalten, bezogen auf das Interpolationsintervall [-1,1] , Werte der Lebesgue-Konstante
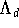 , die Schranken dafür darstellen, wie stark sich die Werte des
Interpolationspolynoms vom Grad d maximal ändern können,
wenn die Daten
, die Schranken dafür darstellen, wie stark sich die Werte des
Interpolationspolynoms vom Grad d maximal ändern können,
wenn die Daten
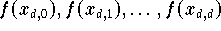 mit additiven Störungen überlagert sind. Angenommen,
mit additiven Störungen überlagert sind. Angenommen,
![\[
\begin{array}{lcl}
P_d & \quad \mbox{interpoliert} \quad & f(x_{d,0}),f(x_{d,1}),\ldots,
f(x_{d,d})\quad\mbox{und} \\[.5ex]
\tilde{P}_d & \quad \mbox{interpoliert} \quad & \tilde{f}(x_{d,0}),
\tilde{f}(x_{d,1}),\ldots,\tilde{f}(x_{d,d}),
\end{array}
\]](pic/f07_0815.gif)
so folgt aus
 ,
,
 , die Abschätzung
, die Abschätzung
![\[
|\tilde{P}_d(x) - P_d(x)| \leq \delta \Lambda_d(K)
\qquad \mbox{für alle} \quad x \in [a,b].
\]](pic/f07_0818.gif)
Wenn z.B. 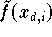 die auf Maschinenzahlen reduzierten Funktionswerte
die auf Maschinenzahlen reduzierten Funktionswerte
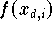 sind, dann wird man z.B. Interpolationspolynome vom Grad 10 noch ohne Schwierigkeiten
verwenden können.
sind, dann wird man z.B. Interpolationspolynome vom Grad 10 noch ohne Schwierigkeiten
verwenden können.
Tabelle: Lebesgue-Konstanten der kubischen Spline-Interpolation (mit
Not-a-knot-Randbedingungen
)
und der Interpolation mit einem einzigen (,,durchgehenden``) Polynom
![\medskip
\begin{table}[hbtp]
\begin{footnotesize}
\caption{Lebesgue-Konstanten der kubischen Spline-Interpolation (mit
{\em Not-a-knot\/}-Rand\-be\-din\-gun\-gen; siehe
Abschnitt~\protect\ref{ss:spline3}) und der Interpolation mit
einem einzigen (](pic/f07_0821.gif)
* * *
Abbildung: Lebesgue-Konstanten
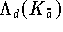 und
und
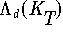 für die Interpolation mit einem Polynom
für die Interpolation mit einem Polynom
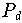 auf den äquidistanten Interpolationsknoten (--) bzw. den
Tschebyscheff-Knoten (--) am Intervall [-1,1].
auf den äquidistanten Interpolationsknoten (--) bzw. den
Tschebyscheff-Knoten (--) am Intervall [-1,1].
* * *
Das exponentielle Anwachsen der Lebesgue-Konstanten
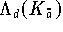 (und damit der Kondition der Polynominterpolation) bringt
die Schwierigkeiten zum Ausdruck, mit denen man bei hohen Polynomgraden und
äquidistanter Knotenanordnung konfrontiert ist.
(und damit der Kondition der Polynominterpolation) bringt
die Schwierigkeiten zum Ausdruck, mit denen man bei hohen Polynomgraden und
äquidistanter Knotenanordnung konfrontiert ist.
Beispiel: Temperaturdaten
Die Tabelle Lebesgue-Konstanten zeigt aber auch (als Vorgriff auf Abschnitt Kubusche Spline Funktion) das vorteilhafte Verhalten der Lebesgue-Konstanten bei der Interpolation immer größer werdender Datenmengen mit kubischen Splinefunktionen. Diese sind auch bei äquidistanter Knotenanordnung und sehr großen Datenmengen ohne Schwierigkeiten verwendbar.
* * *
Die Koeffizienten des Interpolationspolynoms
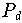 zu vorgegebenen Daten
zu vorgegebenen Daten
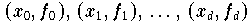
lassen sich prinzipiell durch Lösung eines linearen Gleichungssystems
ermitteln. Der Monombasis
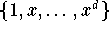 des Raumes
des Raumes
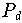 entspricht dabei das lineare Gleichungssystem
entspricht dabei das lineare Gleichungssystem
während die Basis der Tschebyscheff-Polynome auf das lineare Gleichungssystem
für die Koeffizienten
Beispiel:
Kondition der Koeffizientenberechnung
Handelt es sich bei
Die Daten aus dem Jahr 1990 (vgl.\ Abb.~\ref{a1}) lagen alle im Intervall
[0.6, 21.2], aber die Schwankungen im Vergleich zu den langjährigen
Durchschnittswerten führen wegen der schlechten Kondition
(Konditionszahl
Speziell in den Randzonen zeigt sich ein
"Überschwingen"
des Interpolationspolynoms,
das dem intuitiv erwarteten Temperaturverlauf widerspricht.
Abbildung:
Temperaturverlauf in Wien: Monatsmittelwerte des Jahres 1990
(Datenpunkte
* * *
Kondition der Koeffizientenberechnung
Zur quantitativen Charakterisierung der Datenfehlerempfindlichkeit der Koeffizienten
der Matrix
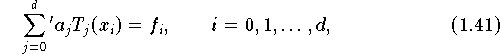
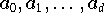 führt.
führt.
Die Matrix
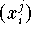 des Gleichungssystems
(1.40)
ist eine Vandermondesche Matrix,
die bereits für mittelgroße Polynomgrade d
numerisch singulär ist, das Gleichungssystem
(1.40)
wird dann praktisch unlösbar. Andererseits ist die Matrix
des Gleichungssystems
(1.40)
ist eine Vandermondesche Matrix,
die bereits für mittelgroße Polynomgrade d
numerisch singulär ist, das Gleichungssystem
(1.40)
wird dann praktisch unlösbar. Andererseits ist die Matrix
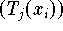 bezüglich eines speziell definierten inneren Produktes eine orthogonale Matrix - ist also
optimal konditioniert - und das Gleichungssystem
(1.41)
ist besonders einfach zu lösen, wenn man als Interpolationsknoten
bezüglich eines speziell definierten inneren Produktes eine orthogonale Matrix - ist also
optimal konditioniert - und das Gleichungssystem
(1.41)
ist besonders einfach zu lösen, wenn man als Interpolationsknoten
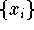 entweder die
Tschebyscheff-Nullstellen
oder die
Tschebyscheff-Extrema
verwendet (vgl. Abschnitt
Koeffizientenberechnung
).
entweder die
Tschebyscheff-Nullstellen
oder die
Tschebyscheff-Extrema
verwendet (vgl. Abschnitt
Koeffizientenberechnung
).
Beispiele:
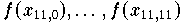 um Temperaturwerte,
die man während der 12 Monate eines Jahres beobachtet hat,
dann kann die Interpolation auf den äquidistanten Knoten 1, 2, ... , 12
durch ein Polynom vom Grad 11 zu unangenehmen Überraschungen führen.
Die langjährigen Monatsdurchschnittswerte zeigen gute Übereinstimmung mit einem
sinusförmigen Temperaturverlauf.
Sie können daher durch ein Polynom vom Grad 11 relativ unproblematisch interpoliert werden.
um Temperaturwerte,
die man während der 12 Monate eines Jahres beobachtet hat,
dann kann die Interpolation auf den äquidistanten Knoten 1, 2, ... , 12
durch ein Polynom vom Grad 11 zu unangenehmen Überraschungen führen.
Die langjährigen Monatsdurchschnittswerte zeigen gute Übereinstimmung mit einem
sinusförmigen Temperaturverlauf.
Sie können daher durch ein Polynom vom Grad 11 relativ unproblematisch interpoliert werden.
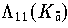 = 51.2 ) dazu, daß die Werte
= 51.2 ) dazu, daß die Werte
![P_d(x), \, x \in [1,12]](pic/f07_0834.gif) , des Interpolationspolynoms hier im Intervall [-18, 22] liegen.
, des Interpolationspolynoms hier im Intervall [-18, 22] liegen.

 ) und durchschnittliche
Monatsmittel 1951 - 1990 (Datenpunkte
) und durchschnittliche
Monatsmittel 1951 - 1990 (Datenpunkte
 ); jeweils
interpoliert durch ein Polynom vom Grad 11.
); jeweils
interpoliert durch ein Polynom vom Grad 11.
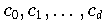 in
(1.40)
bzw.
in
(1.40)
bzw.
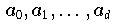 in
(1.41)
kann man die Konditionszahl
in
(1.41)
kann man die Konditionszahl
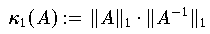
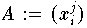 bzw.
bzw.
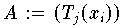 heranziehen. Abb.
Konditionszahlen der Koeffizientenbestimmung
zeigt diese Konditionszahlen für niedrige Polynomgrade und verschiedene
Kombinationen der Basiswahl und der Stützstellenanordnung (in [-1,1]):
heranziehen. Abb.
Konditionszahlen der Koeffizientenbestimmung
zeigt diese Konditionszahlen für niedrige Polynomgrade und verschiedene
Kombinationen der Basiswahl und der Stützstellenanordnung (in [-1,1]):
| BM | --- | Monombasis
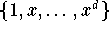 , ,
|
| BT | --- | Tschebyscheff-Basis
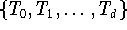 , ,
|
| Kä | --- | äquidistante Knoten, |
| KT | --- | Tschebyscheff-Nullstellen als Knoten. |
Abbildung: Konditionszahlen der Koeffizientenbestimmung in Abhängigkeit von Polynomgrad, Basis (Monome und Tschebyscheff-Polynome) und Knotenanordnung (äquidistant und Tschebyscheff-Nullstellen). Man beachte den logarithmischen Maßstab auf der Ordinate!
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]