 handeln kann. Aus dieser Tatsache kann man zwei wichtige Folgerungen
ableiten:
handeln kann. Aus dieser Tatsache kann man zwei wichtige Folgerungen
ableiten:
Autor: Stefan Huber
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Wenn zwei Polynome vom Grad d dieselben d+1 Datenpunkte
interpollieren,
dann folgt aus der Unisolvenz-Eigenschaft der univariaten Polynome,
daß es sich höchstens um zwei verschiedene Darstellungen
desselben Polynoms bezüglich verschiedener Basen des
 handeln kann. Aus dieser Tatsache kann man zwei wichtige Folgerungen
ableiten:
handeln kann. Aus dieser Tatsache kann man zwei wichtige Folgerungen
ableiten:
 - praktisch ausgeführt werden.
- praktisch ausgeführt werden.
Die Form, bei der ein univariates Polynom als Linearkombination der
Monome 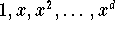 dargestellt wird
(9.6)
- die
Potenzform
eines Polynoms vom Grad d -,
ist die mathematische Standardform,
wie sie vor allem für theoretische
Untersuchungen verwendet wird. Für numerische Berechnungen sind
aber oft andere Darstellungen weit günstiger, wie z.B. die Form
dargestellt wird
(9.6)
- die
Potenzform
eines Polynoms vom Grad d -,
ist die mathematische Standardform,
wie sie vor allem für theoretische
Untersuchungen verwendet wird. Für numerische Berechnungen sind
aber oft andere Darstellungen weit günstiger, wie z.B. die Form
die man durch Entwicklung von
(9.6)
um die Stelle c erhält. Die Form
(9.8)
der Polynomdarstellung kann - bei geeigneter Wahl der Entwicklungsstelle
c - numerisch wesentlich stablier sein als die Form
(9.6).
Beispiel (Polynom-Auswertung)
Der Parabel 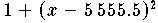 entspricht in der Form
(9.8) das Polynom
entspricht in der Form
(9.8) das Polynom
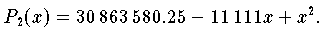
Berechnet man die Werte
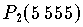 und
und 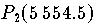 mit Zahlen aus
mit Zahlen aus
 ,
so erhält man aufgrund von Auslöschungseffekten nur die grob
fehlerhaften Resultate 0 bzw. 100. Die Auswertung der Form
(9.8)
,
so erhält man aufgrund von Auslöschungseffekten nur die grob
fehlerhaften Resultate 0 bzw. 100. Die Auswertung der Form
(9.8)
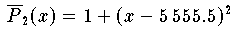
ist in diesem Fall ohne Auslöschung möglich und liefert die exakten Werte 1.25 und 2.
Es empfiehlt sich generell, die Form (9.8) der Potenzform (9.6) vorzuziehen, wobei die Wahl der Entwicklungsstelle c möglichst im Schwerpunkt jener x-Werte erfolgen sollte, für die das Polynom ausgewertet werden soll.
Die
Lagrange-Polynome
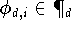 (die auch Lagrangesche Basis- oder
Elementarpolynome
genannt werden) bilden eine Basis
(die auch Lagrangesche Basis- oder
Elementarpolynome
genannt werden) bilden eine Basis
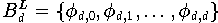
des Vektorraums
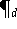 . Sie sind für eine gegebene Menge
. Sie sind für eine gegebene Menge
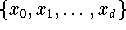 von d+1 voneinander verschiedenen Punkten - den
Interpolationsknoten - durch folgende Eigenschaften charakterisiert:
von d+1 voneinander verschiedenen Punkten - den
Interpolationsknoten - durch folgende Eigenschaften charakterisiert:
Die Lagrange-Polynome
 , deren Existenz und Eindeutigkeit nach den Resultaten des
Abschnitts 6.6
gesichert ist, kann man z.B. durch ihre
Linearfaktorenzerlegung
darstellen:
, deren Existenz und Eindeutigkeit nach den Resultaten des
Abschnitts 6.6
gesichert ist, kann man z.B. durch ihre
Linearfaktorenzerlegung
darstellen:
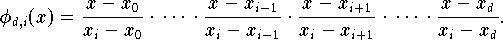 .
.
Beispiel (Lagrange-Polynome)
In
Abb. 9.4
ist das Lagrange-Polynom
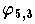 für zwei verschiedene Anordnungen der Interpolationsknoten
dargestellt: für äquidistante Knoten auf [-1,1] und die
Nullstellen des Tschebyscheff-Polynoms
für zwei verschiedene Anordnungen der Interpolationsknoten
dargestellt: für äquidistante Knoten auf [-1,1] und die
Nullstellen des Tschebyscheff-Polynoms
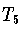 (siehe Abb. 9.7).
(siehe Abb. 9.7).
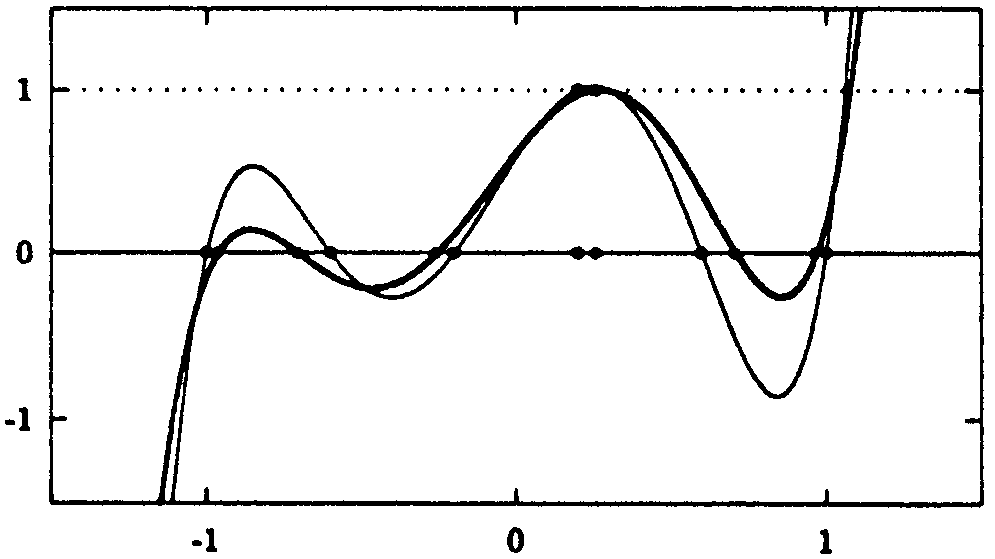
Abb. 9.4:
Lagrange-Polynom
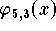 für die Tschebyscheff-Knoten (--) und die äquidistanten
Knoten (--) auf [-1.1]
für die Tschebyscheff-Knoten (--) und die äquidistanten
Knoten (--) auf [-1.1]
Diskrete Orthogonalität: Bezüglich des inneren Produktes
wobei 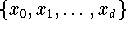 die Menge der Interpolationsknoten ist, gilt:
die Menge der Interpolationsknoten ist, gilt:
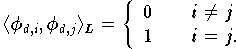
Die Lagrange-Basis
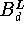 ist also bezüglich
(9.10)
ein Orthonormalsystem.
ist also bezüglich
(9.10)
ein Orthonormalsystem.
Basis der Bernstein-Polynome
Die Bernstein-Polynome
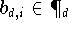 sind durch
sind durch
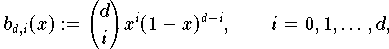
definiert. Auch sie bilden eine Basis
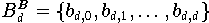
des linearen Raumes
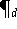 . Dementsprechend besitzt jedes Polynom
. Dementsprechend besitzt jedes Polynom
 eine Darstellung bezüglich der Bernstein-Basis
eine Darstellung bezüglich der Bernstein-Basis
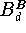 :
:
Die Koeffizienten
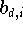 nennt man aber zumeist nicht Bernstein-, sondern
Bézier-Koeffizienten;
(9.11)
bezeichnet man als
Bézier-Darstellung.
nennt man aber zumeist nicht Bernstein-, sondern
Bézier-Koeffizienten;
(9.11)
bezeichnet man als
Bézier-Darstellung.
Nullstellen: hat genau zwei reelle Nullstellen:
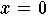
| ist eine i-fache Nullstelle, |
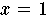
| ist eine (d-i)-fache Nullstelle. |
Maxima:
![$b_{d,i}$ hat in $[0,1]$](pic/f07_0236.gif) hat in [0,1] genau ein Maximum an der Stelle x=i/d.
hat in [0,1] genau ein Maximum an der Stelle x=i/d.
Basis der Tschebyscheff-Polynome
Von allen Systemen orthogonaler Polynome, die eine Basis des Raumes
 bilden, spielen in der Numerischen Datenverarbeitung die
Tschebyscheff-Polynome
bilden, spielen in der Numerischen Datenverarbeitung die
Tschebyscheff-Polynome
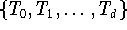 die wichtigste Rolle:
die wichtigste Rolle:
Mit Hilfe der Rekursion
(9.12)
kann man 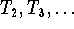 ermitteln:
ermitteln:
In
(9.13)
wird jedes Tschebyscheff-Polynom
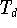 bezüglich der Monombasis
bezüglich der Monombasis
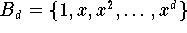 ausgedrückt. Umgekehrt kann man jedes Monom
ausgedrückt. Umgekehrt kann man jedes Monom
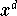 durch die Elemente der Tschebyscheff-Basis
durch die Elemente der Tschebyscheff-Basis
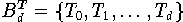
ausdrücken:
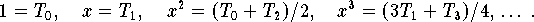
Jedes beliebige Polynom
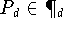 Kann dementsprechend als Linearkombination von Tschebyscheff-Polynomen
dargestellt werden:
Kann dementsprechend als Linearkombination von Tschebyscheff-Polynomen
dargestellt werden:
wobei die Koeffizienten dieser Darstellung mit jenen der Monom-Darstellung (9.6) im allgemeinen nicht übereinstimmen.
Notation (Summe mit Strich)
Die Konvention, den ersten Koeffizienten zu halbieren, was durch
 ausgedrückt wird, stammt von der Reihendarstellung beliebiger
Funktionen durch
ausgedrückt wird, stammt von der Reihendarstellung beliebiger
Funktionen durch
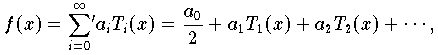
womit sich eine einheitliche Formel
(10.13)
für alle Koeffizienten
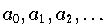 ergibt.
ergibt.
In manchen Situationen ist auch die Darstellung
bei der erster und letzter Summand halbiert werden, zweckmäßig.
Notation (Zweigestrichene Summe)
Durch 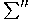 wird ausgedrückt, daß bei der Summation der erste
und der letzte Summand halbiert werden
(vgl. 9.15):
wird ausgedrückt, daß bei der Summation der erste
und der letzte Summand halbiert werden
(vgl. 9.15):
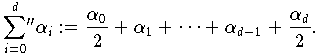
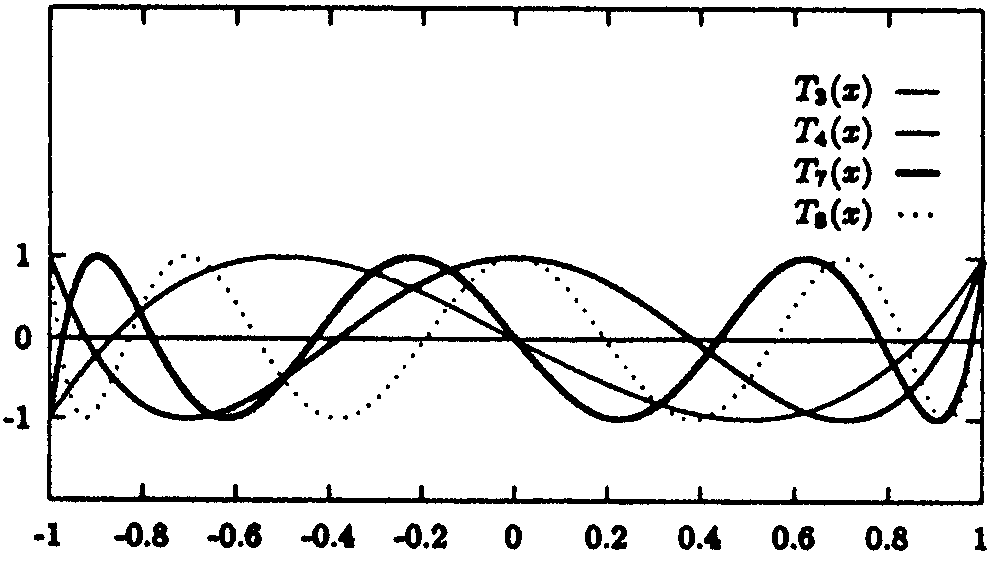
Abb. 9.5: Tschebyscheff-Polynome
 auf [-1,1]
auf [-1,1]
Nullstellen:
 hat in [-1,1] d Nullstellen (siehe
Abb. 9.6 und
Abb. 9.7)
hat in [-1,1] d Nullstellen (siehe
Abb. 9.6 und
Abb. 9.7)
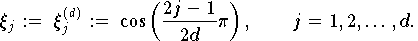
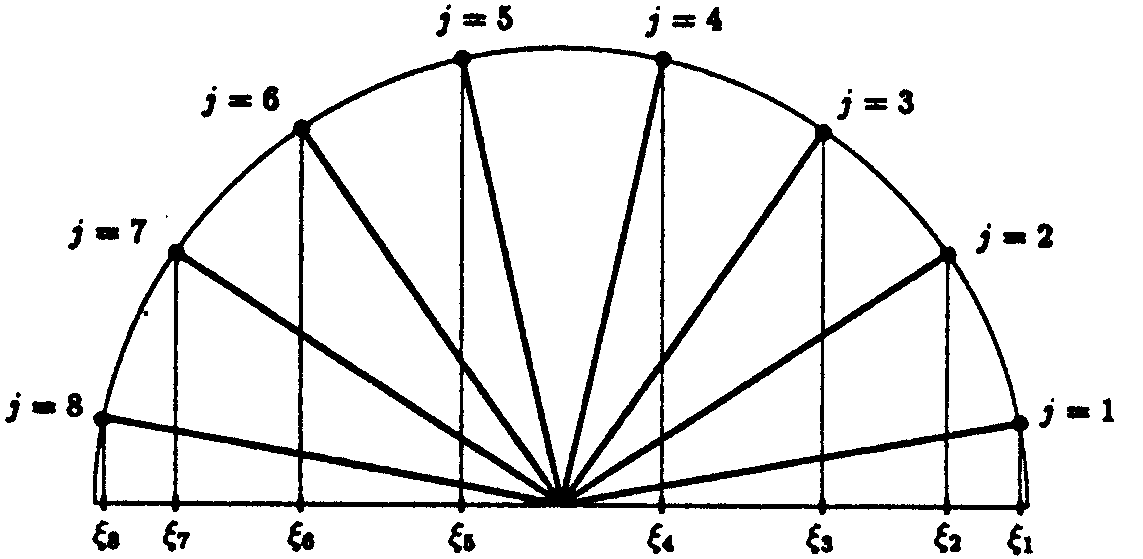
Abb. 9.6: Nullstellen
 des Tschebyscheff-Polynoms
des Tschebyscheff-Polynoms

Abb. 9.7: Nullstellen der
Tschebyscheff-Polynome
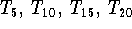
Extrema: Im Intervall [-1,1] gibe es d+1 Stellen (Extrema)
wo 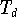 ein Minimum oder ein Maximum besitzt
(Rivlin [341]).
Dabei gilt
ein Minimum oder ein Maximum besitzt
(Rivlin [341]).
Dabei gilt

d.h., an jeder Maximumstelle hat
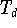 den Wert 1 und an jeder Minimumstelle den Wert -1. Auf [-1,1] gilt
somit
den Wert 1 und an jeder Minimumstelle den Wert -1. Auf [-1,1] gilt
somit 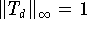 .
.
Die Nullstellen und Extrema der Tschebyscheff-Polynome spielen als Interpolationsknoten eine wichtige Rolle.
Terminologie (Tschebyscheff-Abszissen)
Falls im
folgenden von Tschebyscheff-Abszissen oder -Knoten
die Rede ist, handelt es sich um die Nullstellen von
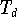 . Zur genaueren Unterscheidung wird auch von
Tschebyscheff-Extrema gesprochen.
. Zur genaueren Unterscheidung wird auch von
Tschebyscheff-Extrema gesprochen.
Diskrete Orthogonalität: Bezüglich des speziellen inneren Produktes
wobei 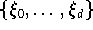 die Menge der Nullstellen von
die Menge der Nullstellen von
 ist, gilt
(Cheney [35]):
ist, gilt
(Cheney [35]):
Eine ähnliche Eigenschaft gibt es auch bezüglich des inneren Produkts
wobei  die Menge der Extrema von
die Menge der Extrema von
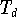 ist. Hier gilt:
ist. Hier gilt:
Bemerkung (Kontinuierliche Orthogonalität)
Die kontinuierliche Orthogonalität der
Tschebyscheff-Polynome wird erst in
Kapitel 10
behandelt (vgl. Formel
(10.11)
).
Minimax-Eigenschaft: Die Tschebyscheff-Polynome sind unter allen Polynomen durch folgende Eigenschaft ausgezeichnet:
Satz
9.3.1 (Tschebyscheff)
die kleinste Maximumnorm auf dem Intervall [-1,1]. Wegen
Beweis:
Von allen Polynomen
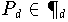 mit einem Anfangskoeffizienten
mit einem Anfangskoeffizienten
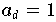 hat das Polynom
hat das Polynom
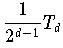
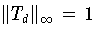 ist dieser Wert
ist dieser Wert
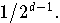
Die sogenannte Minimax-Eigenschaft der Tschebyscheff-Polynome kann man
auch anders formulieren: Unter allen Polynomen mit
 auf [-1,1] und
auf [-1,1] und
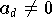 hat das Tschebyscheff-Polynom
hat das Tschebyscheff-Polynom
 mit
mit
 den größten führenden Koeffizienten und das
Monom
den größten führenden Koeffizienten und das
Monom  mit
mit 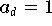 den kleinsten. Eine Entwicklung (Darstellung) nach
Tschebyscheff-Polynomen hat daher den Vorteil des schellsten
Abklingverhaltens der Koeffizenten. Entwicklungen mit schnell
abklingenden Koeffizienten ermöglichen sehr "kompakte"
Approximationen, wenn man die Terme mit vernachlässigbar (betrags)
kleinen Koeffizienten wegläßt.
den kleinsten. Eine Entwicklung (Darstellung) nach
Tschebyscheff-Polynomen hat daher den Vorteil des schellsten
Abklingverhaltens der Koeffizenten. Entwicklungen mit schnell
abklingenden Koeffizienten ermöglichen sehr "kompakte"
Approximationen, wenn man die Terme mit vernachlässigbar (betrags)
kleinen Koeffizienten wegläßt.
Eine ausführliche Behandlung wichtiger Eigenschaften der Tschebyscheff-Polynome findet man z.B. in Büchern von Rivlin [341] sowie Fox und Parker [199].
Autor: Stefan Huber
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]