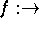 durch ein Polynom
durch ein Polynom
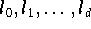 mittels Interpolation zu approximieren, muß man d+1
lineare Funktionale
mittels Interpolation zu approximieren, muß man d+1
lineare Funktionale
 vorgeben und dann jenes Polynom
vorgeben und dann jenes Polynom
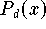 bestimmen, das die Interpolationsbedingungen
bestimmen, das die Interpolationsbedingungen
Autor: Stefan Huber
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Um eine gegebene Funktion
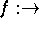 durch ein Polynom
durch ein Polynom
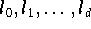 mittels Interpolation zu approximieren, muß man d+1
lineare Funktionale
mittels Interpolation zu approximieren, muß man d+1
lineare Funktionale
 vorgeben und dann jenes Polynom
vorgeben und dann jenes Polynom
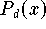 bestimmen, das die Interpolationsbedingungen
bestimmen, das die Interpolationsbedingungen
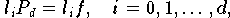
erfüllt. Im Prinzip könnte man die Koeffizienten von
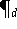 durch Lösung des Gleichungssystems
(9.3)
mit den Basisfunktionen
durch Lösung des Gleichungssystems
(9.3)
mit den Basisfunktionen
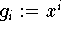 und den Werten
und den Werten
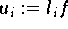 erhalten, müßte dabei jedoch einen
erhalten, müßte dabei jedoch einen
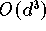 -Aufwand in Kauf nehmen. In wichtigen Spezialfällen gelingt es,
das Polynom
-Aufwand in Kauf nehmen. In wichtigen Spezialfällen gelingt es,
das Polynom
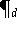 explizit darzustellen und dessen Koeffizienten durch Algorithmen
erheblich geringerer Komplexität zu bestimmen.
explizit darzustellen und dessen Koeffizienten durch Algorithmen
erheblich geringerer Komplexität zu bestimmen.
Für den Fall
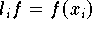 mit paarweise verschiedenen Knoten
mit paarweise verschiedenen Knoten
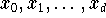 kann man den Ansatz
kann man den Ansatz
machen, wobei
 die Lagrange-Polynome vom Grad d zur Knotenmenge
die Lagrange-Polynome vom Grad d zur Knotenmenge
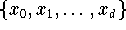 sind. Da die Polynome
sind. Da die Polynome
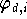 definitionsgemäß die Eigenschaft
(9.9)
besitzen, gilt
definitionsgemäß die Eigenschaft
(9.9)
besitzen, gilt
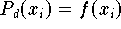 :
:
 ist das gesuchte Interpolationspolynom. Die Darstellung
(9.22)
bezeichnet man als die Lagrangesche Form des
Interpolationspolynoms.
ist das gesuchte Interpolationspolynom. Die Darstellung
(9.22)
bezeichnet man als die Lagrangesche Form des
Interpolationspolynoms.
Die Lagrangesche Darstellung macht die lineare Struktur des
Interplationspolynoms
 bezüglich der Werte
bezüglich der Werte
 deutlich sichtbar, da die Basisfunktionen
deutlich sichtbar, da die Basisfunktionen
 nur von den Interpolationsknoten
nur von den Interpolationsknoten
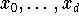 abhängen. Für algorithmische Anwendungen kommt die
Lagrange-Form jedoch wegen des Aufwandes, den die Berechnung der
Funktion
abhängen. Für algorithmische Anwendungen kommt die
Lagrange-Form jedoch wegen des Aufwandes, den die Berechnung der
Funktion
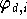 erfordert, nur selten in Betracht.
erfordert, nur selten in Betracht.
Eine Basis des
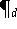 , die besondere Vorteile für die Numerische Datenverarbeitung
besitzt, wird von den Tschebyscheff-Polynomen
, die besondere Vorteile für die Numerische Datenverarbeitung
besitzt, wird von den Tschebyscheff-Polynomen
 abgebildet. Die Koeffizienten
abgebildet. Die Koeffizienten
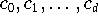 der Darstellung
(9.15)
sind durch das lineare Gleichungssystem
der Darstellung
(9.15)
sind durch das lineare Gleichungssystem
festgelegt. Die Lösung des Gleichungssystems
(9.23)
erhält man durch sehr einfache Formeln, wenn man als
Interpolationsknoten die Tschebyscheff-Nullstellen
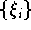 oder die Tschebyscheff-Extrema
oder die Tschebyscheff-Extrema
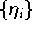 verwenden kann, da sich in diesen Fällen die diskrete
Orthogonalität der Tschebyscheff-Polynome ausnutzen
läßt.
verwenden kann, da sich in diesen Fällen die diskrete
Orthogonalität der Tschebyscheff-Polynome ausnutzen
läßt.
Mulitpliziert man z.B. im Falle der Tschebyscheff-Extrema beide Seiten des linearen Gleichungssystems
von links mit der Matrix
![\left( \begin{array}{ccccc}
\frac{1}{2} T_0(\eta_0) & T_0(\eta_1) & \cdots &
T_0(\eta_{d-1}) & \frac{1}{2} T_0(\eta_d) \\[1.5ex]
\frac{1}{2} T_1(\eta_0) & T_1(\eta_1) & \cdots &
T_1(\eta_{d-1}) & \frac{1}{2} T_1(\eta_d) \\
\vdots & \vdots & & \vdots & \vdots \\
\frac{1}{2} T_d(\eta_0) & T_d(\eta_1) & \cdots &
T_d(\eta_{d-1}) & \frac{1}{2} T_d(\eta_d)
\end{array} \right) ,](pic/f07_0331.gif)
dann erhält man wegen der diskreten Orthogonalität (9.21)

Da die Tschebyscheff-Polynome auch in der Form
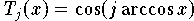
dargestellt werden können, erhält man für die Tschebyscheff-Extrema (9.17) als Interpolationsknoten den besonders einfachen Ausdruck
für die Koeffizienten von (9.24).
Analog erhält man für die Tschebyscheff-Nullstellen (9.14) das lineare Gleichungssystem
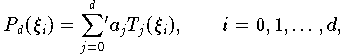
für die Koeffizienten
 der Darstellung
(9.14).
Aus der diskreten Orthogonalität
(9.19)
der Tschebyscheff-Polynome folgt
der Darstellung
(9.14).
Aus der diskreten Orthogonalität
(9.19)
der Tschebyscheff-Polynome folgt
Software (Berechnung eines interpolierenden Polynoms)
Die 2 Unterprogramme NAG/e01aef und NAG/e02aff berechnen zu
vorgegebenen Datenpunkten die Koeffizienten der Tschebyscheff-Darstellung
des entsprechenden Interpolationspolynoms. Während das Unterprogramm
NAG/e02aff nur für die Interpolation an den Tschebyscheff-Extrema
geeignet ist, können mittels NAG/e01aef Funktionswerte - und auch
eventuell zusätzlich vorgegebene Ableitungswerte - an beliebig
verteilten, paarweise verschiedenen Abszissen interpoliert werden.
Das Unterprogramm SLATEC/polint berechnet für beliebig
verteilte Datenpunkte die Koeffizienten - die sogenannten
dividierten Differenzen - der Newton-Darstellung des
zugehörigen Interpolationspolynoms
(de Boor [40]).
Beispiel (Schwierig zu approximierende Funktion)
ist auf [0,1] beliebig oft differenzierbar, die Folge der
Interpolationspolynome
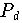 auf den Tschebyscheff-Knoten konvergiert daher für
auf den Tschebyscheff-Knoten konvergiert daher für
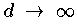 gegen
gegen
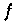 (vgl.
Abschnitt 6.7.7
). Es ist also gewährleistet, daß es für jede Toleranz
(vgl.
Abschnitt 6.7.7
). Es ist also gewährleistet, daß es für jede Toleranz
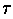 ein Polynom
ein Polynom 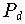 gibt, das von
gibt, das von 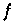 um nicht mehr als
um nicht mehr als  abweicht. Selbst für bescheidene Werte von
abweicht. Selbst für bescheidene Werte von
 sind hierfür allerdings sehr hohe Polynomgrade erforderlich (siehe
Abb. 9.8,
Abb. 9.9 und
Abb. 9.10).
sind hierfür allerdings sehr hohe Polynomgrade erforderlich (siehe
Abb. 9.8,
Abb. 9.9 und
Abb. 9.10).
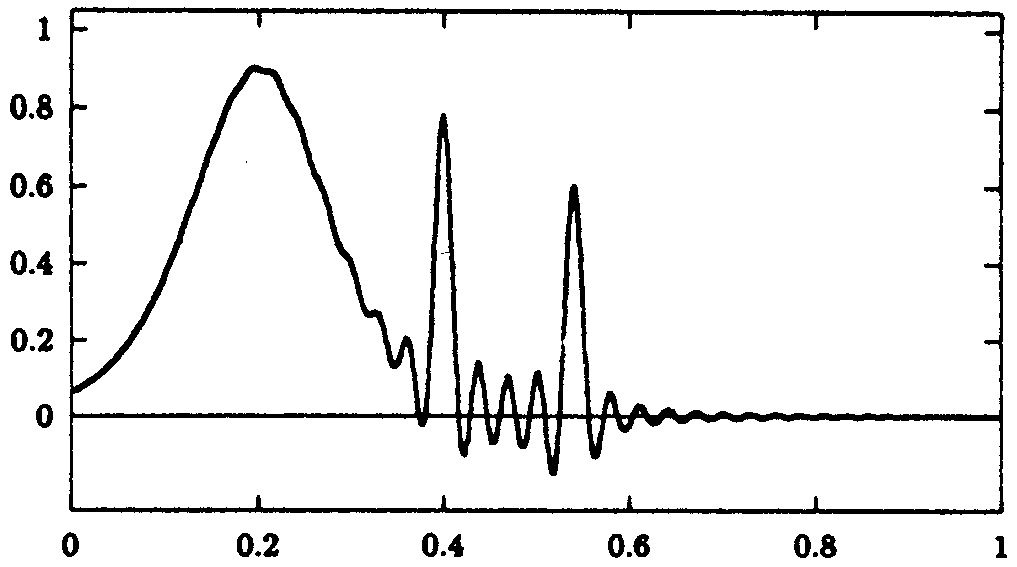
Abb. 9.8: Interpolation der Funktion
(9.27)
durch ein Polynom zu den 100 auf [0,1] transformierten
Tschebyscheff-Abszissen.
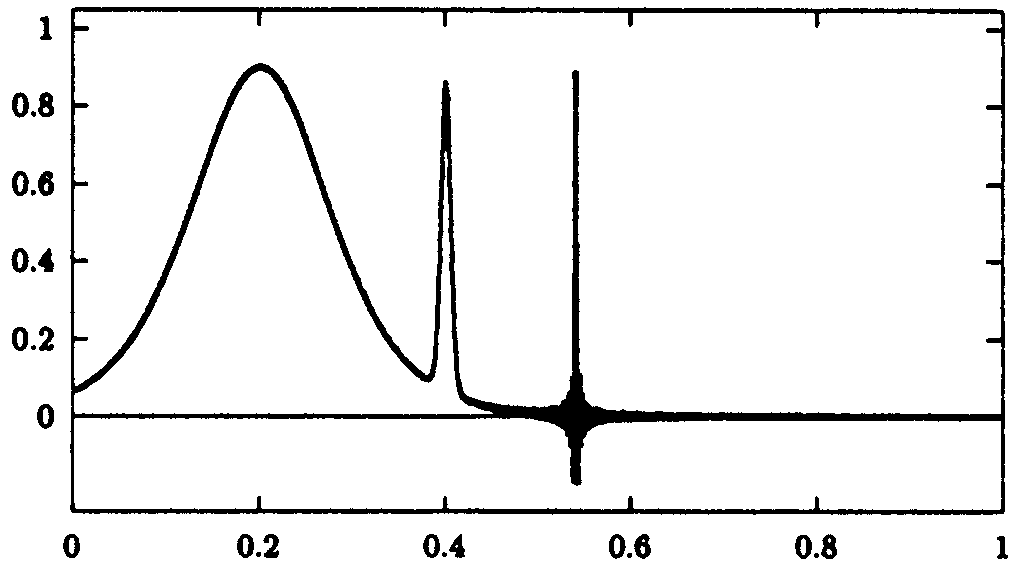
Abb. 9.9: Interpolation der Funktion
(9.27)
durch ein Polynom zu den 1000 auf [0,1] transformierten
Tschebyscheff-Abszissen.
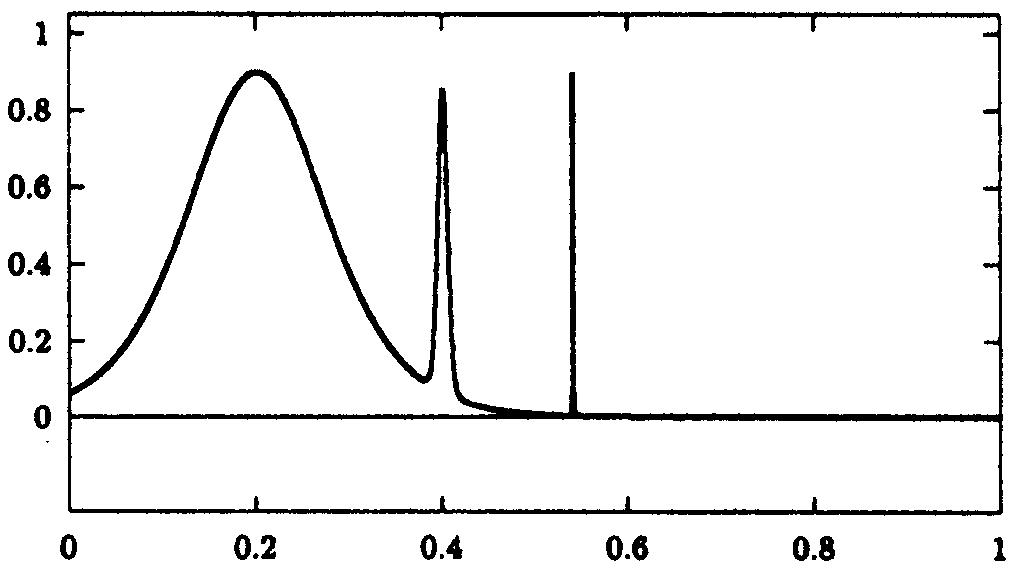
Abb. 9.10: Interpolation der Funktion
(9.27)
durch ein Polynom zu den 10 000 auf [0,1] transformierten
Tschebyscheff-Abszissen.
Autor: Stefan Huber
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]