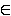
 d und
d und 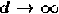 )
stets zum Ziel führt, wenn man z.B. annimmt, daß f auf [a,b] stetig
ist. Der folgende Satz von K. Weierstraß (1885) scheint die Bejahung dieser
Frage nahezulegen:
)
stets zum Ziel führt, wenn man z.B. annimmt, daß f auf [a,b] stetig
ist. Der folgende Satz von K. Weierstraß (1885) scheint die Bejahung dieser
Frage nahezulegen:
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Es erhebt sich die Frage, ob die Vorgangsweise des globalen Erhöhens
der Parameteranzahl der Approximationsfunktion (Pd 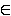
 d und
d und 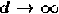 )
stets zum Ziel führt, wenn man z.B. annimmt, daß f auf [a,b] stetig
ist. Der folgende Satz von K. Weierstraß (1885) scheint die Bejahung dieser
Frage nahezulegen:
)
stets zum Ziel führt, wenn man z.B. annimmt, daß f auf [a,b] stetig
ist. Der folgende Satz von K. Weierstraß (1885) scheint die Bejahung dieser
Frage nahezulegen:
Für jede Funktion f 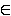 C[a , b] gibt es zu jedem beliebigen
C[a , b] gibt es zu jedem beliebigen
 > 0 ein Polynom P
> 0 ein Polynom P 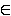
 , das
, das

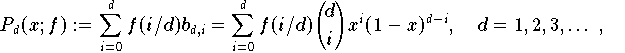 Formel (7.7.1)
Formel (7.7.1) ) zu einem Polynom einer vorgegebenen Approximationsgüte
kommen kann.
) zu einem Polynom einer vorgegebenen Approximationsgüte
kommen kann.
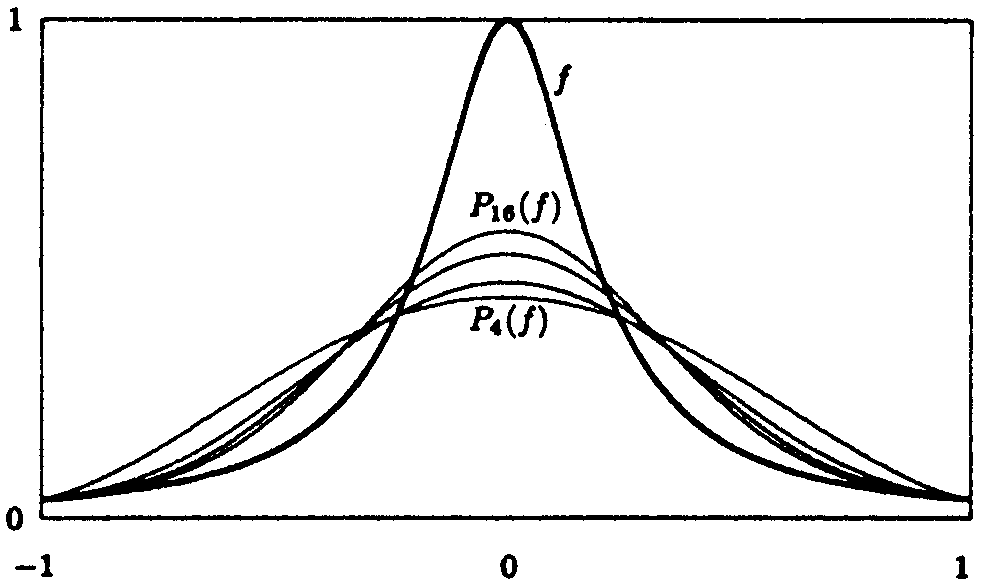
Definition (Knotenmatrix)
Das a priori (unabhängig von den approximierenden Funktionen) festgelegte
Stützstellenschema einer unendlichen Folge {P0, P1, P2,...} von Interpolationspolynomen
![\[
K = \left( \begin{array}{llll}
x_{0,0} & & & \\
x_{1,0} & x_{1,1} & & \\
x_{2,0} & x_{2,1} & x_{2,2} & \\
\vdots & \vdots & \vdots & \ddots
\end{array}
\right)
\]](pic/f07_0716.gif)
Die Wahl einer universellen, vom konkreten Approximationsproblem unabhängigen
Knotenmatrix beeinflußt in sehr starkem Maß die Eigenschaften eines
darauf aufbauenden (nicht-adaptiven) Interpolationsalgorithmus. Je umfassender
z.B. die Menge jener Funktionen ist, bei der die Konvergenz der
Interpolationspolynome 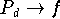 mit
mit 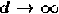 sichergestellt ist,
desto größer ist der Anwendungsbereich des entsprechenden Interpolationsalgorithmus.
Die Konvergenz garantiert nämlich für jede geforderte Approximationsgenauigkeit
r>0, daß der Interpolationsalgorithmus, der auf einem sukzessiven Berechnen der Polynome
zu den Knoten {xd,0, xd,1, ...., xd,d}, d=0,1,2,.., beruht, nach endlich vielen
Schritten erfolgreich abgebrochen werden kann (wobei Fragen des Rechenaufwandes
und der Rundungsfehlereinflüsse zunächst nicht in Betracht gezogen werden).
Nach dem Satz von Weierstraß könnte man vermuten, daß die Funktionenklassen,
für die Konvergenz
sichergestellt ist,
desto größer ist der Anwendungsbereich des entsprechenden Interpolationsalgorithmus.
Die Konvergenz garantiert nämlich für jede geforderte Approximationsgenauigkeit
r>0, daß der Interpolationsalgorithmus, der auf einem sukzessiven Berechnen der Polynome
zu den Knoten {xd,0, xd,1, ...., xd,d}, d=0,1,2,.., beruht, nach endlich vielen
Schritten erfolgreich abgebrochen werden kann (wobei Fragen des Rechenaufwandes
und der Rundungsfehlereinflüsse zunächst nicht in Betracht gezogen werden).
Nach dem Satz von Weierstraß könnte man vermuten, daß die Funktionenklassen,
für die Konvergenz 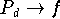 garantiert werden kann, alle stetigen Funktionen
f
garantiert werden kann, alle stetigen Funktionen
f 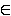 C[a,b] umfaßt. Diese naheliegende Vermutung ist jedoch
falsch, wie der folgende Satz zeigt.
C[a,b] umfaßt. Diese naheliegende Vermutung ist jedoch
falsch, wie der folgende Satz zeigt.
Satz (Faber)
Es existiert keine universelle Knotenmatrix K, mit der die zugehörigen Interpolationspolynome
für jede Funktion f 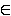 C[a,b] gegen f konvergieren.
C[a,b] gegen f konvergieren.
Die Aussage des Satzes von Faber steht nicht im Widerspruch zum
Satz von Weierstraß, da man für jede einzelne
Funktion f 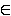 C[a,b] durchaus eine Knotenmatrix K angeben kann, für die
Pj(f) gegen f gilt. Man muß dazu nur die in [a,b] gelegenen Nullstellen der Fehlerfunktion
der bezüglich der Maximumnorm bestapproximierenden Polynome P0*, P1*, P2*,... in K zusammenfassen.
C[a,b] durchaus eine Knotenmatrix K angeben kann, für die
Pj(f) gegen f gilt. Man muß dazu nur die in [a,b] gelegenen Nullstellen der Fehlerfunktion
der bezüglich der Maximumnorm bestapproximierenden Polynome P0*, P1*, P2*,... in K zusammenfassen.
Wenn man die auf definierte Funktionenklasse F gegenüber C[a,b] verkleinert, so gelingt es,
universelle Knotenmatrizen zu finden, bei denen die Konvergenz  für jede Funktion
f
für jede Funktion
f 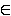 F gilt. Für die erforderlichen Konvergenzuntersuchungen werden die
wichtigen Begriffe des Lebesgue-Funktionen und die -Konstanten benötigt.
F gilt. Für die erforderlichen Konvergenzuntersuchungen werden die
wichtigen Begriffe des Lebesgue-Funktionen und die -Konstanten benötigt.
Definition (Lebesgue-Funktion)
Die Betragssumme der Lagrange Polynome 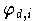 zu den Knoten xd,0, xd,1, ...., xd,d der Knotenmatrix K
zu den Knoten xd,0, xd,1, ...., xd,d der Knotenmatrix K
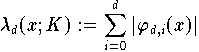

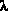 5 der Polynominterpolation zu den sechs Tschebyscheff-Knoten und den sechs äquidistanten Knoten auf [-1,1]
5 der Polynominterpolation zu den sechs Tschebyscheff-Knoten und den sechs äquidistanten Knoten auf [-1,1]
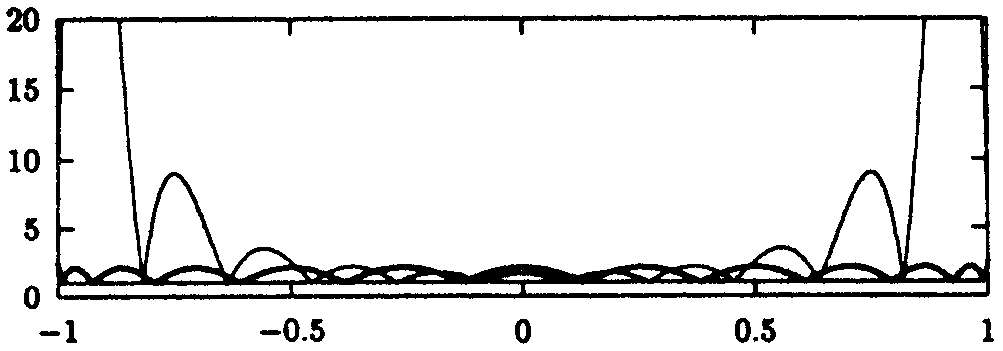
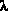 11 der Polynominterpolation zu den 12 Tschebyscheff-Knoten und den 12 äquidistanten Knoten auf [-1,1]
Definition (Lebesgue-Konstante)
11 der Polynominterpolation zu den 12 Tschebyscheff-Knoten und den 12 äquidistanten Knoten auf [-1,1]
Definition (Lebesgue-Konstante)
![\Lambda_d(K) := \max \{ \lambda_d(x;K): x \in [a,b] \}](pic/f07_0727.gif)
Mit Hilfe der Lebesgue-Konstante kann ein Zusammenhang zwischen dem Fehler der Interpolationspolynome
{Pd(f)} bezüglich einer Knotenmatrix K und dem jeweils optimalen (kleinstmöglichen) Approximationsfehler
aller Polynome vom Grad d hergestellt werden.
Die Approximationsqualität einer Folge interpolierender Polynome {Pd} (die durch eine
Knotenmatrix K definiert ist) bezüglich einer Funktion f ist durch den jeweils maximalen Interpolationsfehler
![E_d := E_d(f) := \| e_d \|_{\infty}
= \max \limits_{x \in [a,b]} |P_d(x) - f(x)|,
\qquad d=0,1,2,\dots\,,](pic/f07_0728.gif)
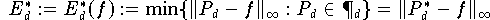
Satz
Für eine Funktion f 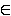 C[a,b] und eine Folge von Interpolationsprolynomen (Pd(f))bezüglich der
Knotenmatrix K gilt:
C[a,b] und eine Folge von Interpolationsprolynomen (Pd(f))bezüglich der
Knotenmatrix K gilt:
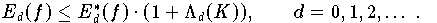 Formel 7.7.2
Formel 7.7.2
Die Lebesgue-Konstanten  , die zwar von der universellen Knotenmatrix K abhängen, aber von f
unabhängig sind, bilden also ein Maß dafür, wie stark der Interpolationsfehler Ed
den optimalen Wert (die untere Schranke) Ed ungünstigstenfalls überschreiten kann. Je kleiner die Lebesgue-Konstanten
einer Knotenmatrix sind, desto näher wird der maximale Interpolationsfehler dem kleinstmöglichen
Approximationsfehler sein.
, die zwar von der universellen Knotenmatrix K abhängen, aber von f
unabhängig sind, bilden also ein Maß dafür, wie stark der Interpolationsfehler Ed
den optimalen Wert (die untere Schranke) Ed ungünstigstenfalls überschreiten kann. Je kleiner die Lebesgue-Konstanten
einer Knotenmatrix sind, desto näher wird der maximale Interpolationsfehler dem kleinstmöglichen
Approximationsfehler sein.
Nach dem Satz von Faber kann die Folge { }, die von f unabhängig ist, nicht beschränkt sein, es muß
}, die von f unabhängig ist, nicht beschränkt sein, es muß
 gegen unendlich gelten. Erdös [187] hat gezeigt, daß es für jede Knotenmatrix K eine Konstante c > 0 gibt,
mit der gilt:
gegen unendlich gelten. Erdös [187] hat gezeigt, daß es für jede Knotenmatrix K eine Konstante c > 0 gibt,
mit der gilt:
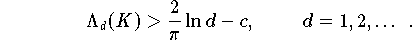
Die Knotenmatrix K als definierender Bestandteil von nicht-adaptiven Approximationsalgorithmen auf
Interpolationsbasis kann - durch ihren Einfluß auf die Konvergenzgeschwindigkeit - die Effizienz
der entsprechenden Algorithmen wesentlich bestimmen. Je näher  (K) an der nicht zu unterschreitenden
Schranke liegt, desto effizienter wird der auf K aufbauende Algorithmus sein. Falls
(K) an der nicht zu unterschreitenden
Schranke liegt, desto effizienter wird der auf K aufbauende Algorithmus sein. Falls  (K)
wesentlich rascher wächst als die untere Schranke, so grenzt dies unter Umständen die Klasse jener
Funktionen, für die Konvergenz
(K)
wesentlich rascher wächst als die untere Schranke, so grenzt dies unter Umständen die Klasse jener
Funktionen, für die Konvergenz 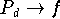 garantiert werden kann, eng ein.
garantiert werden kann, eng ein.
Die Existenz der
"idealen" Knotenmatrix
, die für alle Polynomgrade die kleinstmögliche
Lebesgue-Konstante  liefert, ist zwar theoretisch gesichert (de Boor, Pinnkus [156]), die
Matrix ist aber (noch) nicht bekannt. Eine nicht optimale, aber sehr günstige Folge von
Interpolationsknoten ist durch die Nullstellen (9.16) der Tschebyscheff-Polynome gegeben.
liefert, ist zwar theoretisch gesichert (de Boor, Pinnkus [156]), die
Matrix ist aber (noch) nicht bekannt. Eine nicht optimale, aber sehr günstige Folge von
Interpolationsknoten ist durch die Nullstellen (9.16) der Tschebyscheff-Polynome gegeben.
Die Knotenmatrix 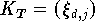 ist auf das Interpolationsintervall [-1,1] bezogen.
Ein anderes Intervall [a,b] kann durch eine affine Transformation der unabhängigen
Veränderlichen auf [-1,19] gebracht werden:
ist auf das Interpolationsintervall [-1,1] bezogen.
Ein anderes Intervall [a,b] kann durch eine affine Transformation der unabhängigen
Veränderlichen auf [-1,19] gebracht werden:

Satz 9.3.7
Die Lebesgue-Konstanten von KT erfüllen die Ungleichung
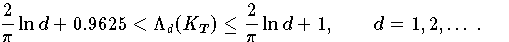 Formel (7.7.3)
Formel (7.7.3)
Selbst für den hohen Polynomgrad d=1000 gilt erst
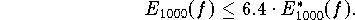
Für 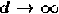 gilt nach dem Satz von Weierstraß
gilt nach dem Satz von Weierstraß
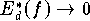 für jede Funktion aus C[a,b]. Wie von Erdös und Vertesi (188) gezeigt wurde,
gibt es für jede Knotenmatrix - also auch für die Tschebyscheff-Knoten - eine Funktion
f
für jede Funktion aus C[a,b]. Wie von Erdös und Vertesi (188) gezeigt wurde,
gibt es für jede Knotenmatrix - also auch für die Tschebyscheff-Knoten - eine Funktion
f 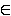 C[a,b], für die die Folge der Interpolationspolynome
auf dem ganzen Intervall [a,b] divergiert (mit Ausnahme eventuell endlich vieler Punkte).
Schränkt man die Funktionenklasse aber etwas ein, z.B. auf jene Funktionen, die auf [-1,1]
Lipschitz-stetig
sind, d.h. auf Funktionen, die für eine Konstante L - die sogenannte
Lipschitz-Konstante
- die Ungleichung
C[a,b], für die die Folge der Interpolationspolynome
auf dem ganzen Intervall [a,b] divergiert (mit Ausnahme eventuell endlich vieler Punkte).
Schränkt man die Funktionenklasse aber etwas ein, z.B. auf jene Funktionen, die auf [-1,1]
Lipschitz-stetig
sind, d.h. auf Funktionen, die für eine Konstante L - die sogenannte
Lipschitz-Konstante
- die Ungleichung
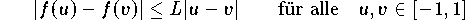
Satz (Jackson)
Für alle auf [-1,1] Lipschitz-stetigen Funktionen mit der Lipschitz-
Konstante L gilt die Fehlerschranke
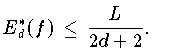 Formel (7.7.4)
Formel (7.7.4)
Für die Knotenmatrix KT erhält man durch Kombination von (7.7.2), (7.7.3) und (7.7.4)
eine obere Schranke für den Approximationsfehler der Interpolationspolynome {Pd},
die für 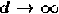 gegen 0 strebt:
gegen 0 strebt:

In der Praxis sind viele wichtigen Funktionen einmal oder öfter stetig differenzierbar.
Für diese Funktionen ist bei Verwendung der Tschebyscheff-Knoten KT die Konvergenz 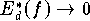 auf jeden Fall sichergestellt.
auf jeden Fall sichergestellt.
Ähnlich günstige Eigenschaften wie die Knotenmatrix der Tschebyscheff-Nullstellen besitzt
die Knotenmatrix 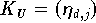 der Tschebyscheff-Extrema (9.17).
der Tschebyscheff-Extrema (9.17).
Interpoliert man unstetige Funktionen mit Sprungstellen durch Polynome zu den Tschebyscheff-
Knoten KT, so tritt ein Überschwingen auf, dessen Maximal- und Minimalamplitude vom
Polynomgrad d (nahezu) unabhängig ist. Diese Besonderheit, die auch bei den Teilsummen von Fourier-
Reihen in der Nähe von Sprungstellen auftritt, heißt
Gibbsches Phänomen
.
Eine Knotenverteilung, die - vor allem aus algorithmischen Gründen - wesentlich
naheliegender ist als jene der Tschebyscheff-Knoten, ist die äquidistante Verteilung

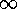 streben, wachsen bei äquidistanter Knotenverteilung
die Lebesgue-Konstanten jedoch exponentiell. Bei äquidistanten Knoten ist selbst die
k-malige Differenzierbarkeit von f nicht hinreichend für die Konvergenz der Interpolationspolynome
streben, wachsen bei äquidistanter Knotenverteilung
die Lebesgue-Konstanten jedoch exponentiell. Bei äquidistanten Knoten ist selbst die
k-malige Differenzierbarkeit von f nicht hinreichend für die Konvergenz der Interpolationspolynome 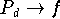 .
Nicht einmal bei beliebig (unendlich) oft differenzierbaren Funktionen ist die Konvergenz
.
Nicht einmal bei beliebig (unendlich) oft differenzierbaren Funktionen ist die Konvergenz
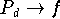 garantiert.
garantiert.
Erst unter der außerordentlich einschränkenden Annahme, daß sich ![f:[a,b]](pic/f07_0762.gif)
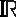 zu einer ganzen Funktion
zu einer ganzen Funktion 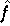 :
: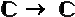 fortsetzen läßt, sodaß die Potenzreihendarstellung von
fortsetzen läßt, sodaß die Potenzreihendarstellung von
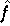 in der gesamten komplexen Ebene
in der gesamten komplexen Ebene 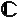 konvergiert, ist die Konvergenz
konvergiert, ist die Konvergenz 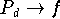 auf äquidistanten
Interpolationsknoten sichergestellt(Hämmerlin,Hoffmann [50]).
auf äquidistanten
Interpolationsknoten sichergestellt(Hämmerlin,Hoffmann [50]).
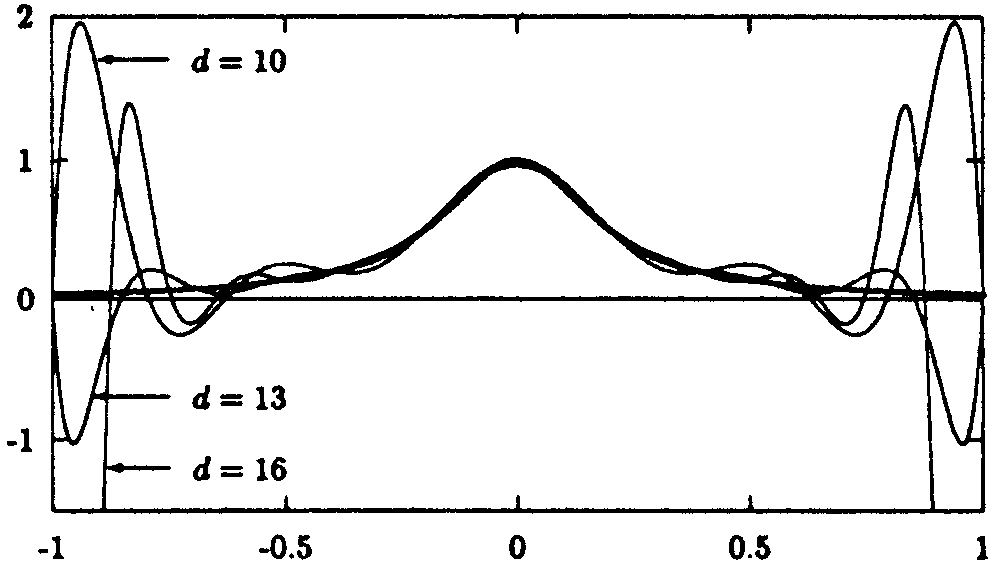
Die Eigenschaft der Interpolationspolynome auf äquidistanten Knoten , bei vielen "harmlosen",
im mathematischen Sinn "sehr glatten" Funktionen für 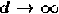 nicht zu konvergieren, macht
sich bereits bei niederen Polynomgraden durch ein starkes Oszillieren des Interpolationspolynoms
bemerkbar (siehe Abb 7.7.4).
nicht zu konvergieren, macht
sich bereits bei niederen Polynomgraden durch ein starkes Oszillieren des Interpolationspolynoms
bemerkbar (siehe Abb 7.7.4).
Ein Nachteil der Interpolation mit äquidistanten Knoten ist auch deren schlechte
Kondition, das empfindliche Reagieren der Werte Pd(x) des Interpolationspolynoms auf
Änderungen der Daten {f(x0),....,f(xd)} (siehe Abschnitt 7.8).
Die Interpolation mit einem Polynom auf gleichabständigen Knoten ist somit nur für relativ
kleine Polynomgrade praktisch brauchbar. Ist die Verwendung äquidistanter Interpolationsknoten
aus irgendeinem Grund erforderlich oder erwünscht, so kommt bei einer größeren Anzahl von
Datenpunkten nur eine stückweise aus Polynomen niedrigerer Grade zusammengesetzte Funktion in
Betracht (siehe Abschnitt 9.4).
Beispiel (Rampenfunktion)
Interpoliert man die Lipschitz-stetigen (aber nicht differenzierbare) Funktion
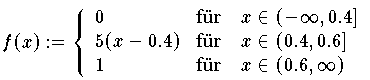 Formel (7.7.5)
Formel (7.7.5)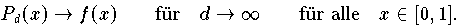
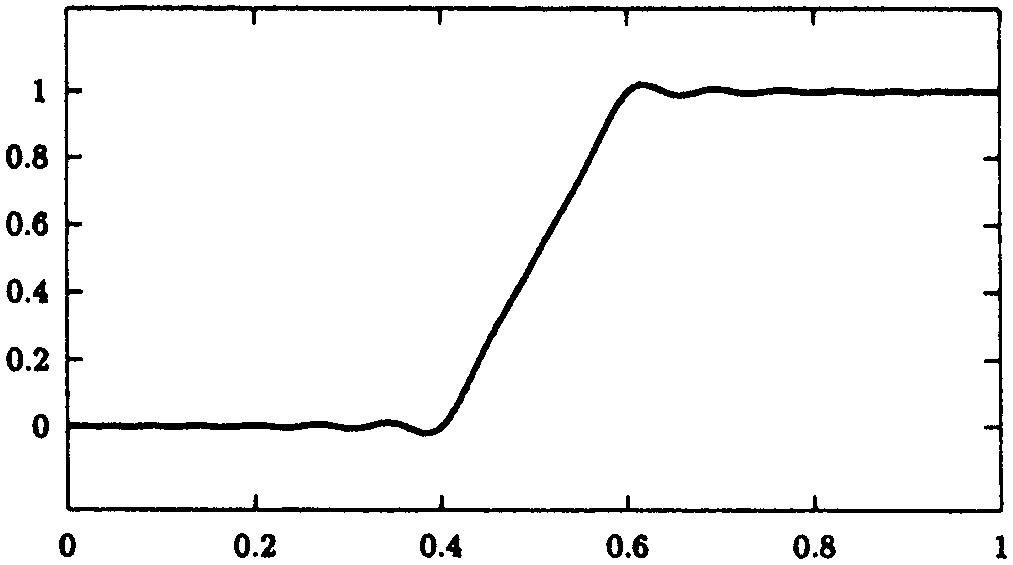
Beispiel (Sprungfunktion)
Interpoliert man die unstetige Sprungfunktion
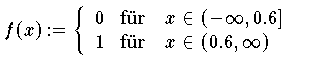 Formel (7.7.6)
Formel (7.7.6)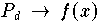 mit Ausnahme der Sprungstelle x = 0.6 (siehe Abb 7.7.6, Abb 7.7.7 und Abb 7.7.8).
In der Nähe der Spungstelle ist in den Abbildungen das Gibbsche Phänomen deutlich zu sehen.
mit Ausnahme der Sprungstelle x = 0.6 (siehe Abb 7.7.6, Abb 7.7.7 und Abb 7.7.8).
In der Nähe der Spungstelle ist in den Abbildungen das Gibbsche Phänomen deutlich zu sehen.
![Interpolation der Sprungfunktion (7.7.6) durch ein Polynom zu den 50 auf [0,1] transformierten Tschebyscheff-Abszissen](pic/f07_0772.gif)
![Interpolation der Sprungfunktion (7.7.6) durch ein Polynom zu den 200 auf [0,1] transformierten Tschebyscheff-Abszissen](pic/f07_0773.gif)
![Interpolation der Sprungfunktion (7.7.6) durch ein Polynom zu den 4000 auf [0,1] transformierten Tschebyscheff-Abszissen](pic/f07_0774.gif)
Beispiel (Divergenz trotz beliebiger Differenzierbarkeit)
Die
Funktion (Runge (345))

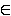 (0.03846,1] gilt. Als Ausdruck der Divergenz tritt mit steigendem
Polynomgrad immer stärker werdendes "Überschwingen" in der Nähe der Intervallendpunkte
-1 und 1 auf (siehe Abb.7.7.4).
(0.03846,1] gilt. Als Ausdruck der Divergenz tritt mit steigendem
Polynomgrad immer stärker werdendes "Überschwingen" in der Nähe der Intervallendpunkte
-1 und 1 auf (siehe Abb.7.7.4).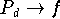 gewährleistet ist, macht die
sehr niedrige Konvergenzgeschwindigkeit den algorithmischen Einsatz äquidistanter Interpolationsknoten
äußerst ineffizient.
gewährleistet ist, macht die
sehr niedrige Konvergenzgeschwindigkeit den algorithmischen Einsatz äquidistanter Interpolationsknoten
äußerst ineffizient.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]