[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
9.9 Auswahl eines iterativen Verfahrens
Bevor man eine Aussage über die Geschwindigkeit der einzelnen Verfahrens machen kann, sollte
man bemerken, daß iterative Verfahren bei schwach besetzen Gleichungssystemen geringere
Genauigkeit liefert als direkte Verfahren.
Dabei ist dies nicht unbedingt ein Nachteil: denn dadurch hat man einen relativ frühen
Abbruchzeitpunkt und kann somit nochmals die Rechenzeit verkürzen.
Dennoch sind schwach besetzte Systeme aufgrund der komprimierten Speicherschemata
ein Problem: die Datenwiederverwendung ist gering (Cache wird nicht ausgelastet), und
durch die Komprimierung geht viel Rechenzeit verloren.
Eigenschaften iterativer Verfahren
In diesem Abschnitt werden die wichtigsten iterativen Verfahren mit deren Charakteristika
überblicksartig dargestellt. Es wird eine Aussage über das Anwendungsgebiet und die Effizienz
getroffen. Denn oft funktioniert ein Verfahren nur auf Grund der Problemstellung. Auch kann
ein Verfahren, obwohl es mehr Operationen benötigt, durchaus effizienter sein, als ein
kürzeres Verfahren. Auch dies ist von der Aufgabenstellung bzw. der Anordnung der Daten
abhängig.
- Jacobi-Verfahren
-
- Gauss-Seidel-Verfahren
-
- SOR-Verfahren
-
- CG-Verfahren
-
- GMRES-verfahren
-
- BiCG-Verfahren
-
- QMR-Verfahren
-
- CGS-Verfahren
-
- BiCGSTAB-Verfahren
-
- Tschebyscheff-Iteration
-
- Besonders einfach in der Verwendung, aber nur langsam konvergierend.
Außer bei starker Diagonaldominanz von A ist das Jacobi-Verfahren
nur als vorkonditionierendes Verfahren für nichtstationäre Methoden zu
empfehlen.
- Parallelisierung ist sehr einfach durchzuführen.
- Schnellere Konvergenz als beim Jacobi-Verfahren, aber trotzdem in vielen
Fällen nicht konkurrenzfähig gegenüber den nichtstationären
Verfahren.
- Anwendbar auf strikt diagonaldominante oder symmetrische positiv
definite Matrizen.
- Eignung zur Parallelisierung ist von der Struktur von A abhängig.
Unterschiedliche Anordnungen der Unbekannten bewirken verschiedene
Grade der Parallelisierbarkeit.
- Beschleunigt die Gauß-Seidel-Konvergenz bei
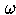 > 1
(Überrelaxation) bzw. kann bei
> 1
(Überrelaxation) bzw. kann bei 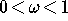 (Unterrelaxation) das Versagen des Gauß-Seidel-Verfahrens
vermeiden und Konvergenz ermöglichen.
(Unterrelaxation) das Versagen des Gauß-Seidel-Verfahrens
vermeiden und Konvergenz ermöglichen.
- Konvergenzgeschwindigkeit ist stark von einer günstigen Wahl des
Parameters
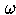 abhängig; der optimale Wert kann
unter Umständen mit dem Spektralradius der
Jacobi-Iterationsmatrix abgeschätzt werden.
abhängig; der optimale Wert kann
unter Umständen mit dem Spektralradius der
Jacobi-Iterationsmatrix abgeschätzt werden.
- Parallelisierung wie beim Gauß-Seidel-Verfahren von der Struktur von A
abhängig.
- Anwendbar nur auf symmetrische, positiv definite Systeme.
- Konvergenzverhalten von der Konditionszahl
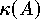 abhängig; bei
bestimmten Eigenwertkonstellationen kann überlineares
Konvergenzverhalten eintreten.
abhängig; bei
bestimmten Eigenwertkonstellationen kann überlineares
Konvergenzverhalten eintreten.
- Parallelisierbarkeit ist weitgehend von A unabhängig, hängt aber
stark von der vorkonditionierenden Matrix ab.
- Anwendbar auf nichtsymmetrische Matrizen.
- Das kleinste Residuum wird in einer festen Anzahl von Schritten
erreicht, die Iterationsschritte werden aber immer rechenaufwendiger.
- Neustarts sind nötig, um den wachsenden Speicherbedarf und den
Rechenaufwand in Grenzen zu halten. Die Wahl des richtigen Zeitpunkts
für diesen Eingriff hängt von
A und der Vorkonditionierung ab und
verlangt vom Anwender Erfahrung und Wissen.
- Anwendbar auf nichtsymmetrische Matrizen.
- Erfordert Matrix-Vektor-Produkte mit A und
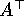 . Das
schließt die Methode für den Fall einer nicht explizit gegebenen
Systemmatrix aus.
. Das
schließt die Methode für den Fall einer nicht explizit gegebenen
Systemmatrix aus.
- Parallelisierung ähnlich wie bei CG-Verfahren; die beiden
Matrix-Vektor-Produkte sind unabhängig voneinander und können
parallel berechnet werden.
- Anwendbar auf nichtsymmetrische Matrizen.
- Regelmäßigere und raschere Konvergenz als beim BiCG-Verfahren.
- Der Rechenaufwand ist etwas höher als beim BiCG-Verfahren.
- Parallelisierung wie beim BiCG-Verfahren.
- Anwendbar auf nichtsymmetrische Matrizen.
- Konvergiert (divergiert andernfalls aber auch) meist doppelt so
schnell wie das
BiCG-Verfahren. Die Konvergenz ist oft ziemlich unregelmäßig, was
zu einem Verlust an Genauigkeit führen kann.
Neigt zur Divergenz für Startwerte nahe der Lösung.
- Rechenaufwand ähnlich wie beim BiCG-Verfahren, aber
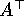 nicht
erforderlich.
nicht
erforderlich.
- Anwendbar auf nichtsymmetrische Matrizen.
- Rechenaufwand ähnlich wie beim BiCG- und beim CGS-Verfahren;
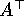 wird nicht benötigt.
wird nicht benötigt.
- Stellt eine Alternative zum CGS-Verfahren dar; führt zu regelmäßigerer
Konvergenz bei nahezu gleicher Konvergenzgeschwindigkeit.
- Anwendbar auf nichtsymmetrische Matrizen.
- Explizite Information über das Spektrum ist notwendig; im
symmetrischen Fall sind die Parameter der Iteration leicht aus den
extremalen Eigenwerten herzuleiten. Die Eigenwerte können entweder
direkt aus der Matrix oder durch einige Iterationsschritte des
CG-Verfahrens abgeschätzt werden.
- Die angepaßte Tschebyscheff-Methode kann in Kombination mit CG-
oder GMRES-Verfahren
verwendet werden, indem die Iteration mit ihr fortgesetzt wird,
sobald passende Information über das Spektrum von A verfügbar ist.
Die Auswahl der ,,besten`` Lösungsmethode für eine gegebene Klasse von
Problemen setzt nicht nur Kenntnisse des theoretischen Hintergrunds voraus
(siehe z.B. Freund, Golub, Nachtigal []),
sondern ist auch eine Frage von Versuchen und Erfahrung. Sie ist auch
vom verfügbaren Speicherplatz (GMRES-Verfahren), von der Verfügbarkeit von
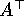 (BiCG-, QMR-Verfahren) und vom Aufwand
für Matrix-Vektor-Produkte
im Vergleich zu inneren Produkten abhängig.
(BiCG-, QMR-Verfahren) und vom Aufwand
für Matrix-Vektor-Produkte
im Vergleich zu inneren Produkten abhängig.
Vergleich iterativer Verfahren
Um verschiedene iterative Verfahren experimentell zu vergleichen, wurden die
TEMPLATES-Programme (siehe Abschnitt ) so modifiziert,
daß sie auch große Matrizen im CRS-Format verarbeiten können. Für die
Matrix-Operationen wurden SPARSKIT-Programme (siehe
Abschnitt ) verwendet.
Als Testdaten dienten die Matrizen BCSSTK14 und WATT1 der
Harwell-Boeing-Collection ), die
schon beim Vergleich der Speicherformate
verwendet wurden. Dort befindet sich auch eine Beschreibung dieser Matrizen.
Durchführung der Tests
Zuerst wurde das Produkt der Matrix mit dem Vektor
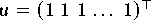 gebildet.
Das Ergebnis dieser Multiplikation
wurde dann als rechte Seite b des Gleichungssystems verwendet.
gebildet.
Das Ergebnis dieser Multiplikation
wurde dann als rechte Seite b des Gleichungssystems verwendet.
Die numerischen Lösungen der einzelnen Programme wurden mit dem Vektor u
verglichen. Die Beträge der maximalen Abweichungen stehen in den Tabellen
in der Spalte "Fehler".
Die Tests wurden alle auf einer typischen HP-Workstation mit einer
Maximalleistung von 50 Mflop/s durchgeführt. Die Zeitangaben in den
Tabellen stellen sicher
nicht die optimalen Werte dar, die auf diesem Rechner möglich wären, sondern
dienen lediglich dem Vergleich der Verfahren untereinander.
Generell kann gesagt werden, daß die Verwendung der einfachen
Jacobi-Vorkonditionierung oft zu einer Effizienzsteigerung, in
manchen Fällen sogar zur Konvergenz eines divergenten Verfahrens führte.
 Tabelle: Testresultate für die symmetrische und positiv definite Matrix BCSSTK14
Tabelle: Testresultate für die symmetrische und positiv definite Matrix BCSSTK14
 Tabelle: Testresultate für die unsymmetrische Matrix WATT1
Tabelle: Testresultate für die unsymmetrische Matrix WATT1
[ < ]
[ globale Übersicht ]
[ Kapitelübersicht ]
[ Stichwortsuche ]
[ > ]
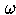 > 1
(Überrelaxation) bzw. kann bei
> 1
(Überrelaxation) bzw. kann bei 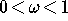 (Unterrelaxation) das Versagen des Gauß-Seidel-Verfahrens
vermeiden und Konvergenz ermöglichen.
(Unterrelaxation) das Versagen des Gauß-Seidel-Verfahrens
vermeiden und Konvergenz ermöglichen.
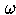 abhängig; der optimale Wert kann
unter Umständen mit dem Spektralradius der
Jacobi-Iterationsmatrix abgeschätzt werden.
abhängig; der optimale Wert kann
unter Umständen mit dem Spektralradius der
Jacobi-Iterationsmatrix abgeschätzt werden.
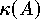 abhängig; bei
bestimmten Eigenwertkonstellationen kann überlineares
Konvergenzverhalten eintreten.
abhängig; bei
bestimmten Eigenwertkonstellationen kann überlineares
Konvergenzverhalten eintreten.
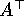 . Das
schließt die Methode für den Fall einer nicht explizit gegebenen
Systemmatrix aus.
. Das
schließt die Methode für den Fall einer nicht explizit gegebenen
Systemmatrix aus.
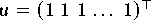 gebildet.
Das Ergebnis dieser Multiplikation
wurde dann als rechte Seite b des Gleichungssystems verwendet.
gebildet.
Das Ergebnis dieser Multiplikation
wurde dann als rechte Seite b des Gleichungssystems verwendet.
 Tabelle: Testresultate für die symmetrische und positiv definite Matrix BCSSTK14
Tabelle: Testresultate für die symmetrische und positiv definite Matrix BCSSTK14 Tabelle: Testresultate für die unsymmetrische Matrix WATT1
Tabelle: Testresultate für die unsymmetrische Matrix WATT1