[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

9.8 Parallelisierung

Da heutzutage Berechnungen extrem komplex sind (z. B. Finite Elemente Methode), ist die Verwendung eines Algorhitmusses oft abhängig, ob dieser Parallelisierbar ist oder nicht.

Wie kann man nun die Berechnungsschritte auf verschiedene Prozessoren aufteilen?

Innere_Produkte
Matrix-Vektor-Produkte
Vorkonditionierung
Ein Beispiel

Innere Produkte

Diese sind leicht zu parallelisieren, indem jeder Prozessor das innere Produkt jeweils korrespondierender Segmente der Vektoren berechnet. Dies nennt man auch Berechnung lokaler innerer Produkte .

Matrix-Vektor-Produkte

Je nach dem, ob die Prozessoren einen gemeinsamen Speicherbereich verwenden, oder eigenen Speicher verwenden muß unterschieden werden:

Gemeinsamer Speicher: die Matrix muß in Streifen zerlegt werden, die auf die Unterteilung der Vektoren abgestimmt sein muß (siehe oben, Inneres Produkt). Jeder Prozessor berechnet dann das Matrix-Vektor Produkt eines Streifens.
Jeder Prozessor hat nur einen Teil des Vektors im Speicher. Dies kann zu Problemen in der Kommunikation zwischen den Prozessoren führen.

Vorkonditionierung

Dies ist das Hauptproblem der Paralleliserbarkeit. Denn gerade bei der Vorkonditionierung müssen alle Daten von einem Prozeß abgearbeitet werden. Eine genaue Übersicht über die Parallelisierung finden Sie im Literaturverzeichnis unter TEMPLATES[3].

Beispiel

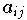Wir betrachten ein lineares Gleichungssystem Ax=b mit einer n x n - Tridiagonalmatrix, d. h. $a_{ij}=0$ = 0 für |i-j| > 1.

Frage:
Wie hoch ist der zusätzliche Speicherbedarf neben den Problemdaten (bei Jacobi und Gauß-Seidel-Verfahren)? Welches der beiden Verfahren (Jacobi- bzw. Gauß-Seidel-Verfahren) läßt sich unmittelbar parallelisieren? Wie hoch ist dabei der theoretisch mögliche "Speedup"? Wieviele Parallelprozessoren benötigt man, um den optimalen "Speedup" auch tatsächlich zu erreichen?

Sowohl das Jacobi- als auch das Gauß-Seidel-Verfahren benötigt zusätzliche n Speicheplätze (Vektor X(1),..,X(n)), neben den speicher für die Problemdaten.

Da beim Gauß-Seidel-Verfahren der Vektor X(neu) mit X(alt) überschrieben wird, wird hierbei kein weiterer Speicher benötigt. Beim Jacobi-Verfahren wird daher im Falle vollbesetzer Matritzen zusätzlich 2n Speicherplatz für xalt(1), ..., Xalt(N) und Xneu(1),...,Xneu(n) benötigt. Bei einer Tridiagonalmatrix würden n+2 Speicherplätze ausreichen (für X(1),..,X(n) und AUX1, AUX2).

Zusammenfassend der Speicherbedarf zusätzlich zu den Problemdaten: $ Matrix voll: [2n] [n], Matrix Tridiagonal: [n+2] [n] $

Das Jacobiverahren läßt sich voll parallelisieren, allerdings um den Preis des vollen Speicherbedarfs von 2n Speicherplätzen (zusätzlich zu den Problemdaten). Die Zuweisungen können idealwerweise so gestaltet werden, daß N Prozessoren parallel arbeiten können. Damit kommt es zu einem "Speedup" von N bei N Prozessoren (und min. N Zeilen/Spalten).

Wegen der sequentiellen Abhängigkeit (die berechneten Werte der Vorrunde werden gleich wiederverwendet), gelingt eine solche Parallelisierung bei Gauß-Seidel nicht. Jedoch kann man dieses Verfahren entsprechend modifizieren: man berechnet eben jede erste, dritte, fünfte, ... Gleichung, anschließend im zweiten Arbeitsgang die geraden Gleichungen. Dann läßt sich jeder Arbeitsgang, als auch der Arbeitsgang selber, parallelisiseren.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]