[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Eine zweite Fehlerquelle stellt sich beispielsweise bei einem System linearer Gleichungen ein , das aus der theoretischen Behandlung einer technischen Aufgabe folgt ; sowohl die Elemente der Matrix als auch die freien Glieder sind nur Näherungsweise mit einer gewissen Genauigkeiten bekannt . Die Ungenauigkeit der Ausgangsdaten ruft Ungenauigkeiten in der Lösung hervor , denn eine in den Grenzen der gegebenen Genauigkeit erfolgende Änderung der Koeffizienten zieht natürlich eine entsprechende Änderung der Lösung nach sich .
Nun werden wir uns ausführlich mit der Untersuchung der
wichtigsten Fehlerquellen bei der Lösung eines Gleichungssystems
befassen .
Dies sind :
Definition : Unter der Konditionszahl cond(A) oder k(A) einer regulären quadratischen Matrix A versteht man die Größe
cond(A) = k(A) := ||A|| ||A-1||.
Führt man weiters die Bezeichnung
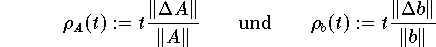
für die relativen Fehler von A und b ein , so schreibt sich die Fehlerabschätzung als
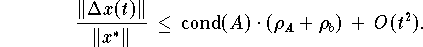
In erster Näherung gilt daher : Die relativen Datenfehler
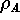 von A und
von A und 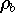 von b wirken sich durch den Faktor cond(A) verstärkt
auf das Resultat des gestörten Gleichungssystems aus . Hat
die Matrix A eine Größe Konditionszahl cond(A) , so
ist das lineare Gleichungssystem Ax = b schlecht konditioniert
.
von b wirken sich durch den Faktor cond(A) verstärkt
auf das Resultat des gestörten Gleichungssystems aus . Hat
die Matrix A eine Größe Konditionszahl cond(A) , so
ist das lineare Gleichungssystem Ax = b schlecht konditioniert
.
( wir nennen eine Matrix schlecht konditioniert , wenn die zugehörige inverse Matrix instabil ist ).
Unter der Konditionszahl cond(A) oder k(A) einer rechteckigen Matrix A versteht man die Größe
cond(A) = k(A) := ||A|| ||A+||.
Für reguläre Matrizen gilt bA = b und daher ||b|| / ||bA || = 1 .
Für singuläre Matrizen , also rang(A) < n , spielt auch der Faktor ||b|| / ||bA || eine wichtige Rolle .Seine geometrische Bedeutung kann man aus der Beziehung
 ,
,
die sich mit Hilfe der Singulärwertzerlegung von A herleiten läßt , erkennen .
Unter der Konditionszahl der rechten Seite b R m bezüglich
eines linearen Gleichungssystems mit der Matrix A
R m bezüglich
eines linearen Gleichungssystems mit der Matrix A Rm*n versteht
man die Größe
Rm*n versteht
man die Größe

Im günstigsten Fall ist cond(b;A) = 1 ,was einem b R(A)
entspricht .
R(A)
entspricht .
In diesem Kapitel werden wir die Auswirkungen von Datenstörungen von A
( Matrix ) oder b ( rechte Seite) eines linearen Gleichungssystems untersuchen .
Im Fall einer gestörten Matrix und einer ungestörten rechten Seite
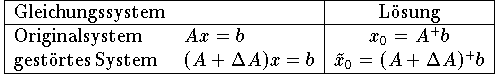
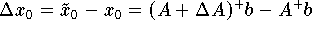
müssen drei Fälle unterschieden werden . Je nach dem , ob die Störung
Im Fall einer ungestörten Matrix aber einer gestörten rechten Seite , liegt folgende Situation vor :
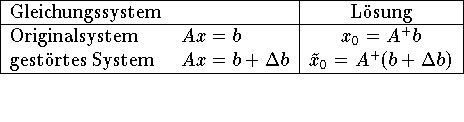
Aus der Definition der Störung der Lösung folgt
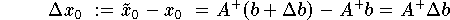
und daher folgt

Diese Abschätzung des absoluten Fehlers zeigt , daß bereits eine kleine Änderung der rechten Seite b zu einer großen Änderung der Lösung x0 führen kann , wenn der Verstärkungsfaktor groß ist .
Falls rang(A+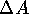 ) = rang(A) bzw. die dazu äquivalenten Bedingungen
) = rang(A) bzw. die dazu äquivalenten Bedingungen
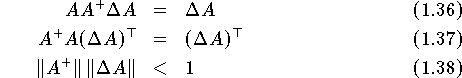
gelten, so erhält man für den relativen Fehler Qx folgende Abschätzung
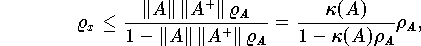
wobei

die relative Störung der Matrix A charakterisiert .
Gilt rang(A+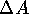 ) > rang(A) , so gilt die Abschätzung
) > rang(A) , so gilt die Abschätzung
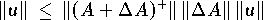
und schließlich
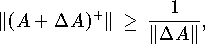
woraus der unstetige Zusammenhang zwischen A und A+ folgt.
Falls rang(A+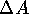 ) <= rang(A) und
) <= rang(A) und  ist , so gilt :
ist , so gilt :
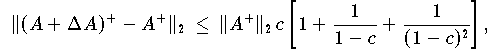
d.h.,in diesem Fall hängt A+ stetig von A ab . Eine Rangverkleinerung ist also unkritisch im Vergleich zu einer Rangvergrößerung.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]