[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Die im Integrations-Applet verwendeten Verfahren

Im folgenden soll nochmals ein kurzer Überblick über die im Beispiel-Applet implementierten Integrationsverfahren gegeben werden.

Riemannsche Summen

Die Riemann-Summen führen unmittelbar auf die Definition des Integralbegriffes (Riemann-Integrale) überhaupt. Eine Riemann-Summe auf einem Intervall [a,b] ist, wie schon andernorts erwähnt, definiert als:

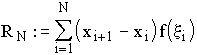
$R_N:=\overset{N}\to{\underset{i=1}\to{\sum }}\left( x_{i+1}-x_i\right) f\left(\xi _i\right) $
wobei N die Anzahl der (beliebig wählbaren) Teilintervalle und xii jeweils einen (ebenfalls beliebigen) Punkt innerhalb eines solchen darstellt.

Wählt man nun die Teilintervalle gleich breit, gelangt man zu folgendem Algorithmus (der natürlich noch keinen Integrationsalgorithmus im eigentlichen Sinn darstellt:

function r_summe(n) // n sei die Anzahl der Teilintervalle
begin
  summe := 0;
  h := (b - a) / n;
  for x := a to (b-h) step h do 
    summe := summe + f( xi(x, x+h) );
            // xi sei ein Wert im Intervall [x,x+h]
  summe := summe * h;
  r_summe := summe;
end;

Im Applet stehen vier verschiedene Möglichkeiten zur Auswahl von xi aus dem Intervall [x,x+h] zur Verfügung (li sei x, re sei x+h - linke und rechte Intervallschranke):

Die Abschätzung der Genauigkeit der errechneten Näherung wird mittels einer nichtadaptiv-iterativen Strategie durchgeführt.

Keplersche Faßregel

Aus der Keplerschen Faßregel ging später die Simpson-Regel hervor, die zu den abgeschlossenen Newton-Cotes-Formeln gehört. Die Näherung des Integrals wird in einem einzigen Schritt berechnet:

I := (b - a) / 6 * (f(a) + 4 * f((a + b) / 2) + f(b));

Zusammengesetzte Trapezregel

Die Formel der zusammengesetzten l+1-Punkt-Trapezregel führt auf folgende Funktion:

function trapez(l);
begin
  h := (b-a) / l;
  sum := h * ( f(a) / 2 );
  for k := 1 to (l - 1) do sum := sum + h * ( f( a + k * h ) );
  sum := sum + h * f(b) / 2;
  trapez := sum;
end;

Die Genauigkeit des Ergebnisses wird wie bei den Riemannschen Summen abgeschätzt.

Erreichen der erforderten Genauigkeit

Um den Fehler der Integralnäherung geringer als den geforderten Wert (epsilon) zu halten, wird bei den Riemann-Summen und der Trapezregel (iterativ) eine iterierte nicht-adaptive Diskretisierungsstrategie angewandt:

const MaxIterationen = Maximale Anzahl der Iterationen

begin
  iterationen := 0;
  wert_alt := kleinste darstellbare Zahl;
  wert_neu := größte darstellbare Zahl;
  n := 1; // Anzahl der Unterteilungen
  while (iterationen < MaxIterationen) and (abs(wert_neu-wert_alt) > epsilon) do
  begin
    iterationen := iterationen + 1;
    wert_alt := wert_neu;
    wert_neu := r_summe(n) // oder wert_neu := trapez(n);
    n := 2 * n; // Anzahl der Intervallunterteilungen verdoppeln
  end while;
  if abs(wert_neu - wert_alt) > epsilon then 
    write('Die gewählte Genauigkeit konnte nicht erreicht werden.');
end; // Ergebnis steht in wert_neu

Es gilt allerdings zu beachten, daß diese Art der Fehlerschätzung falsche Ergebnisse liefert, wenn die Differenz zweier Näherungen kleiner als der Fehler zum exakten Wert ist; besser wäre die Auswertung einer speziell auf das jeweilige Verfahren zugeschnittenen Fehlerschätzungsformel (wie z.B. der Euler-Maclaurinschen Summenformel für die zusammengesetzte Trapezregel).

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]