[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Inhaltsverzeichnis Kapitel 7.4.2 Riemann-Summen

  • Definition: Riemann-Summen
  • Definition: Riemann-Integral
  • Beispiel für die Riemann-Summen

    • 7.4.2 Riemann-Summen

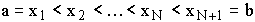
    Definition (Riemann-Summen): Durch jede Unterteilung des Intervalls [a,b] in N Teilintervalle,

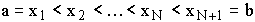
    $a=x_1<x_2<\ldots <x_n<x_{n+1}=b$
    und jede Auswahl von N Punkten
    $\xi _i\in \left[ x_i,x_{i+1}\right] ,\,i=1,2,\ldots ,N$
    wird eine Riemann-Summe definiert:
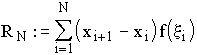
    $R_N:=\overset{N}\to{\underset{i=1}\to{\sum }}\left( x_{i+1}-x_i\right) f\left(\xi _i\right) $

    Definition (Riemann-Integral):

    Falls alle Folgen {RN} von Riemann-Summen mit

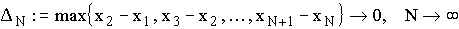
    $\Delta _N\,:=\max \left\{ x_2-x_1,x_3-x_4,\ldots ,x_{N+1}-x_N\right\} \rightarrow 0,\,\,\,N\rightarrow \infty $


    einen gemeinsamen Grenzwert R besitzen, dann bezeichnet man f auf [a,b] als Riemann-integrierbar und definiert das Riemann-Integral als diesen Grenzwert
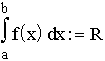
    $\int\limits_a^bf\left( x\right) \,dx:=R$

    Eine einfache Möglichkeit, eine Folge von Riemann-Summen zu erzeugen, ergibt sich, wenn man das Intervall [a,b] in gleichlange Teilintervalle unterteilt. Man wählt nun entweder den linken oder den rechten Endpunkt des entstandenen Teilintervalls aus und erhält auf diese Weise zwei konvergente Riemann-Summen, die beide den gleichen Grenzwert besitzen. Diesen Grenzwert kann man als Näherung für If ansehen.

    In der Praxis zeigt sich aber, daß die Konvergenz dieser beiden Riemann-Summen in der Regel extrem langsam ist.

    Beispiel (Riemann-Summen)
    Dies soll in Form eines interaktiven Beispiels gezeigt werden.

    [ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]