[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
[ Thomas Theußl ]

6.8.1 Polynom(Sub)splines

Fordert man für stückweise definierte Polynome höhere Stetigkeit beziehungsweise höhere Differenzierbarkeit an den Teilungspunkten, so führt dies zu den Spline-Funktionen:

Definition (Polynom-Splines, polynomiale Splinefunktionen) Polynom-Splines sind stückweise Polynome, bei denen alle Teilpolynome den gleichen Grad d besitzen und so zusammengesetzt sind, daß an den Teilungspunkten x1,x2,..,xk, den inneren Knoten der Knotenmenge {xi}, die links- und rechtsseitigen Ableitungen bis zur (d-1)-ten Ordnung übereinstimmen:

s(xi-) = s(xi+)

s'(xi-) = s'(xi+)

:

s(d-1)(xi-) = s(d-1)(xi+)

mit i = 1,2,...k-1.

Die Forderung nach der (d-1)-maligen stetigen Differenzierbarkeit führt dazu, daß dieses Verfahren zu einem globalen Interpolationsverfahren wird, mit dem Nachteil, daß die Funktion zum starken Oszillieren neigt. Sollte man hingegen noch fordern, daß auch die d-te Ableitung übereinstimmt, so würde es sich nicht mehr um stückweise definierte, sondern um ein durchgehendes Polynom handeln (vgl. not-a-knot Bedingungen ).

Fordert man hingegen nur Übereinstimmungen bis zur m-ten Ableitung, mit m<d-1, so spricht man von Subsplines. Wobei hier von besonderer Bedeutung die kubischen Subsplines (s.a. Akima Interpolation) sind.

Definition (Kubische Subsplinefunktion) Eine stückweise aus kubischen Polynomen bestehende Funktion s mit

s(xi-)=s(xi+) und s'(xi-)=s'(xi+), i=1,2,...,k-1

heißt Subsplinefunktion oder defekte Splinefunktion.

Darstellung von Polynomsplines

Hermite Darstellung kubischer Splines

Kubische Splines können sehr effizient durch die Angabe von Wertetripeln

(x0,f0,s'0),(x1, f1,s'1),...,(xk,fk, s'k)

dargestellt werden. Die Berechnung der Koeffizienten der in den Intervallen definierten kubischen Funktionen

P3(x) = a0 + a1(x-xi-1) + a2(x-xi-1)2 + a3(x-xi-1)3

erfolgt mittels folgenden Formeln:

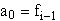
$a_0=f_{i-1}$

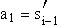
$a_1=s_{i-1}^{^{\prime }}$

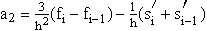
$a_2=\frac 3{h^2}(f_i-f_{i-1})-\frac 1h(s_i^{^{\prime }}+s_{i-1}^{^{\prime }})$

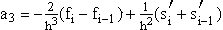
$a_3=-\frac 2{h^3}(f_i-f_{i-1})+\frac 1{h^2}(s_i^{^{\prime }}+s_{i-1}^{^{\prime }})$

Abgebrochene Potenzfunktionen

Da sich die einzelnen Polynome nur in den d-ten Ableitungen unterscheiden, kann man diese sehr effizient darstellen, indem man nur die Koeffizienten des ersten Polynoms, und danach nur mehr die Sprünge in den d-ten Ableitungen abspeichert. Die mathematische Form dieser Darstellung erhält man mit Hilfe der abgebrochenen bzw. abgeschnittenen Potenzen vom Grad d:

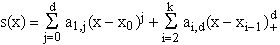
$s(x)=\dsum\limits_{j=0}^da_{1,j}(x-x_0)^j+\dsum\limits_{i=2}^ka_{i,d}(x-x_{i-1})_{+}^d$

Die abgebrochenen Potenzen bilden zusammen mit den Monomen eine Basis des Raumes der polynomialen Splinefunktionen vom Grad d mit den inneren Knoten x1,x2,...,xk-1

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]