Computernumerik am WWW

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
[ Thomas Theußl ]

6.8.2 Anwendungen von Polynomsubsplines

Diese Interpolationsmethode verwendet kubische Splines, wobei die Stetigkeitsforderungen darauf beschränkt werden, daß nur Funktionswerte und erste Ableitungen an den Interpolationsstellen übereinstimmen müssen. (Deswegen Subspline-Interpolation, denn für Splines müßten auch noch die zweiten Ableitungen übereinstimmen), wobei die ersten Ableitungen aus den Daten geschätzt werden.

Zur näherungsweisen Bestimmung der Ableitungen an den Interpolationsstellen werden nur der betreffende Datenpunkt und je zwei Punkte auf beiden Seiten verwendet, es handelt sich also um ein lokales Interpolationsverfahren. Diese Bestimmung der Ableitungen beruht auf heuristischen Überlegungen. Zuerst werden die vier Differenzenquotienten

d_i-2,d_i-1,d_i,di+1

der vier Teilintervalle

[x_i-2,x_i-1], [x_i-1,x_i], [x_i,x_i+1], [x_i+1,x_i+2]

gebildet. Je weniger sich nun die zwei links von x_i liegenden Differenzenquotienten unterscheiden, desto eher soll s_i'=d_i-1 gelten. Bei übereinstimmenden Werten soll s_i'=0 gelten. Auf dieser Grundlage definiert man nun

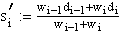
$s_i^{^{\prime }}:=\frac{w_{i-1}d_{i-1}+w_id_i}{w_{i-1}+w_i}$
mit den Gewichten

w_i-1 := |d_i+1-d_i|

w_i := |d_i-1-d_i-2|

wobei sich bei Übereinstimmungen Sonderfälle ergeben:

s_i' := d_i-1, wenn d_i-2 = d_i-1 und d_i <> d_i+1

s_i' := d_i, wenn d_i = d_i+1 und d_i-2 <> d_i-1

s_i' := d_i-1 = d_i, wenn d_i-1 = d_i

Kann s_i' nicht mit dieser Formel ermittelt werden, definiert man
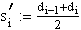
$s_i^{^{\prime }}:=\frac{d_{i-1}+d_i}2$

In den Randintervallen ist diese Formel nicht unmittelbar geeignet, allerdings können aus den Daten auf beiden Seiten je zwei Datenpunkte geschätzt werden, die einem parabelförmigen Kurvenverlauf entsprechen.

Die Vorteile dieser Methode sind die Rechenzeit-Effizienz, da aufgrund der lokalen Definition keine linearen Gleichungsysteme gelöst werden müssen, sowie die Speicherplatz-Effizienz, da zusätzlich zu den gegebenen Daten nur die Hilfspunkte für die Randzonen zu speichern sind.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]