 mit
mit
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Funktionen, die durch Formeln definiert sind, in denen nur endlich viele algebraische Operationen mit der unabhängigen Variablen vorkommen, bezeichnet man als algebraische elementare Funktionen. Diese sind als Approximationsfunktionen (Modellfunktionen) am Computer besonders gut geeignet. Vor allem die Polynome in einer unabhängigen Variablen - die univariaten Polynome - spielen dabei eine zentrale Rolle.
Definition 6.7.1 (Univariates Polynom):
Eine Funktion
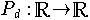 mit
mit
ist ein (reeles) Polynom in einer unabhängigen Variablen.
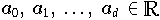 sind die Koeffizienten des Polynoms,
sind die Koeffizienten des Polynoms,
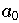 dessen absolutes Glied. Falls
dessen absolutes Glied. Falls
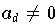 ist, heißt
ist, heißt
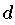 Grad des Polynoms und
Grad des Polynoms und
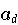 Anfangs- oder höchster Koeffizeint. Ist
Anfangs- oder höchster Koeffizeint. Ist
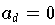 , so heißt
, so heißt
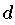 formaler Grad von
formaler Grad von
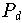 . Polynome vom Grad
. Polynome vom Grad
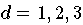 nennt man linear, quadratisch bzw. kubisch.
nennt man linear, quadratisch bzw. kubisch.
Der Funktionsraum
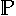 aller Polynome (beliebigen Grades) besitzt z.B. die
Basis der Monome
aller Polynome (beliebigen Grades) besitzt z.B. die
Basis der Monome
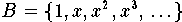
und ist daher unendlich-dimensional; der Raum
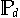 aller Polynome vom Maximalgrad d besitzt z.B. die Basis
aller Polynome vom Maximalgrad d besitzt z.B. die Basis
und ist 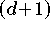 -dimensional. Die Monombasis (9.7)
ist nur eine von unendlich vielen Basen des Vektorraums
-dimensional. Die Monombasis (9.7)
ist nur eine von unendlich vielen Basen des Vektorraums
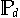 . Weitere, speziell für numerisch-algorithmische Anwendungen wichtige
Basen bilden die Lagrange-, die Bernstein- und vor allem die
Tschebyscheff-Polynome. Sie werden im folgenden behandelt.
. Weitere, speziell für numerisch-algorithmische Anwendungen wichtige
Basen bilden die Lagrange-, die Bernstein- und vor allem die
Tschebyscheff-Polynome. Sie werden im folgenden behandelt.
Eine spezielle Polynom-Darstellungsform ist die Linearfaktorenzerlegung
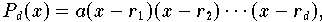
wobei 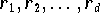 die Nullstellen des Polynoms
die Nullstellen des Polynoms
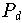 sind. Diese Darstellung beruht nicht auf einer Linearkombination
von Basisfunktionen des Raumes
sind. Diese Darstellung beruht nicht auf einer Linearkombination
von Basisfunktionen des Raumes
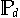 .
.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]