 heißt ein
linearer normierter Raum oder
normierter Raum,
wenn
heißt ein
linearer normierter Raum oder
normierter Raum,
wenn
 ein linearer Raum ist und jedem Element
ein linearer Raum ist und jedem Element
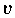 aus
aus
 eine eindeutig bestimmte nichtnegative Zahl
||v||
- die Norm von
eine eindeutig bestimmte nichtnegative Zahl
||v||
- die Norm von
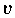 - zugeordnet ist, die folgende Eigenschaften
hat:
- zugeordnet ist, die folgende Eigenschaften
hat:
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Definition: Normierter Raum
Eine Menge
 heißt ein
linearer normierter Raum oder
normierter Raum,
wenn
heißt ein
linearer normierter Raum oder
normierter Raum,
wenn
 ein linearer Raum ist und jedem Element
ein linearer Raum ist und jedem Element
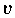 aus
aus
 eine eindeutig bestimmte nichtnegative Zahl
||v||
- die Norm von
eine eindeutig bestimmte nichtnegative Zahl
||v||
- die Norm von
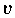 - zugeordnet ist, die folgende Eigenschaften
hat:
- zugeordnet ist, die folgende Eigenschaften
hat:
| 1. | 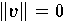 genau dann, wenn
genau dann, wenn
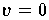 ist
ist
| (Definitheit), | |
| 2. | 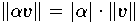 ,
,
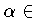
 oder
oder
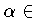 C
C
| (Homogenität), | |
| und | 3. | 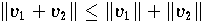
| (Dreiecksungleichung). |
Die geometrische Interpretation der Norm eines Vektors ist seine Länge. Auf Grund ihrer Eigenschaften kann mit jeder Norm eine Metrik definiert werden:
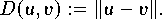
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]