[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Normen für endlich-dimensionale Räume

Die Abstandsdefinition für zwei reelle Zahlen durch die Betragsfunktion

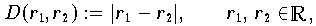
D(r_{1},r_{2}) := |r_{1} - r_{2}|, \qquad r_{1},\,r_{2} \in \R,

kann man für zwei Vektoren u und v des $\R^n$ durch den Euklidischen Abstand (entsprechend der Euklidischen Norm des Differenzvektors) verallgemeinern:

\[ D_2(u,v) := \|u-v\|_2 := \sqrt{(u_{1} - v_{1})^{2} + (u_{2} - v_{2})^{2} + \cdots + (u_{n} - v_{n})^{2}}. \]

Noch allgemeiner definiert man den Abstand von zwei Vektoren $u, v \in \R^{n}$ durch die $l_p$ -Norm ihrer Differenz u-v:

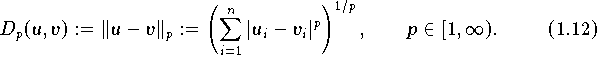
D_p(u,v) := \|u - v\|_{p} := \left(\sum\limits_{i=1}^{n} |u_i-v_i|^p \right)^{1/p}, \qquad p \in [1,\infty).

Als Grenzfall für $p\to\infty$ erhält man die Maximumnorm

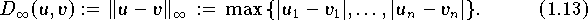
D_{\infty}(u,v) := \|u-v\|_{\infty} \, := \, \max \, \{ |u_1-v_1|, \dots, |u_n-v_n| \}.

Mit ( 1.12 ) und ( 1.13 ) läßt sich im Fall der diskreten Approximation (Datenapproximation) der Abstand einer Modellfunktion $g: \R \to \R$ von gegebenen Datenpunkten

(x_{1},y_{1}), \, (x_{2},y_{2}), \, \ldots, \, (x_{k},y_{k}) \, \in \R^{2}

ermitteln, indem man den Abstand der beiden Vektoren

$$ \left( \begin{array}{c} g(x_{1}) \\ g(x_{2}) \\ \vdots \\ g(x_{k}) \end{array} \right) =: {\Delta}_{k} g \in \R^k \qquad \mbox{und} \qquad \left( \begin{array}{c} y_{1} \\ y_{2} \\ \vdots \\ y_{k} \end{array} \right) =: y \in \R^k $$

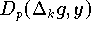durch $D_{p}({\Delta}_{k} g,y)$ definiert.


Große Vorsicht ist bei der Interpretation derartiger Abstandswerte geboten!


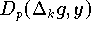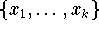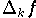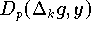Die Maßzahl $D_p (\Delta_k g, y)$ liefert nur Information über den Abstand an der endlichen Menge von Abszissen $\{ x_1, \ldots, x_k \}$ . Falls der Vektor y durch Diskretisierung $\Delta_k f$ einer analytischen Größe f zustandegekommen ist, so liefert $D_p (\Delta_k g, y)$ keinen Hinweis auf die Approximationsqualität von g bezüglich f. Durch die $l_{p}$ -Norm des Vektors

$$ e_{k} \,:=\, [e(x_{1}),\ldots,e(x_{k})]^{\top} \,=\, [f(x_1) - g(x_1), \ldots, f(x_k) - g(x_k)]^{\top} $$

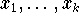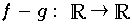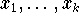der Abweichungen an den Stellen $x_1, \ldots, x_k$ wird nämlich keine Norm für die Funktion $f-g: \R \to \R$ definiert. Für sämtliche Modellfunktionen g, die an den Stellen $x_{1}$,\ldots,$x_{k}$ mit f übereinstimmen, gilt

\| e_{k} \|_{p} = 0,

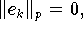
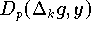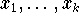ohne daß f - g = 0, also Übereinstimmung f(x) = g(x) für alle $x \in \R$ , gelten müßte. Dementsprechend wird auf diese Weise keine Metrik im Raum der reellwertigen Funktionen definiert. Der Größe des Abstands $D_{p}({\Delta}_{k} g,y)$ kann man keine Information über den Verlauf von e := f - g "zwischen" den Punkten $x_{1}$, \dots, $x_k$ entnehmen. Durch 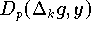$D_{p}({\Delta}_{k} g,y)$ kann man den Abstand der Modellfunktion g von dem zu modellierenden kontinuierlichen Phänomen f nicht charakterisieren.

lp-Normen bei der diskreten Approximation

Die wichtigsten Spezialfälle der $l_{p}$ -Normen für die diskrete Approximation sind durch
p = 2 (Euklidische Norm)
und p = 1 (Betragssummennorm)
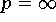gegeben. Die Maximumnorm ( $p = \infty$ ) hat bei der diskreten Approximation keine praktische Bedeutung, da sie für eine Trennung von systematischen und stochastischen Anteilen fehlerbehafteten Datenmaterials nahezu ungeeignet ist.


Die Euklidische Metrik (beruhend auf der $l_{2}$ -Norm, der Euklidischen Norm) wird bei der diskreten Approximation (Signalanalyse) am häufigsten verwendet, denn

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]