 , so geht man implizit davon aus, daß jeder
Funktionswert f(t) bzw. jeder Datenpunkt
, so geht man implizit davon aus, daß jeder
Funktionswert f(t) bzw. jeder Datenpunkt
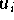 die gleiche
Bedeutsamkeit besitzt und daher keine spezielle Gewichtung
einzelner Werte erforderlich ist.
die gleiche
Bedeutsamkeit besitzt und daher keine spezielle Gewichtung
einzelner Werte erforderlich ist.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Verwendet man die bisher besprochenen Normen zur Definition einer Distanzfunktion
 , so geht man implizit davon aus, daß jeder
Funktionswert f(t) bzw. jeder Datenpunkt
, so geht man implizit davon aus, daß jeder
Funktionswert f(t) bzw. jeder Datenpunkt
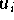 die gleiche
Bedeutsamkeit besitzt und daher keine spezielle Gewichtung
einzelner Werte erforderlich ist.
die gleiche
Bedeutsamkeit besitzt und daher keine spezielle Gewichtung
einzelner Werte erforderlich ist.
Es gibt Fälle, wo a priori bekannt ist, daß z.B. einzelne Datenpunkte
durch genauere Messungen gewonnen wurden, während andere mit größeren
Meßfehlern behaftet sind. In einer solchen Situation sollte eine
Gewichtung der Datenpunkte erfolgen:
Gewichte
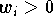 bzw. Gewichtsfunktionen
bzw. Gewichtsfunktionen
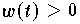 sollten den Datenpunkten so zugeordnet werden, daß genauere Werte einen
größeren Einfluß auf das Entfernungsmaß
sollten den Datenpunkten so zugeordnet werden, daß genauere Werte einen
größeren Einfluß auf das Entfernungsmaß
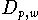 erhalten als ungenauere Werte. Dazu benötigt man
erhalten als ungenauere Werte. Dazu benötigt man
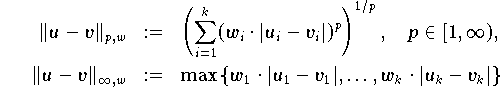
bzw.
gewichtete
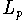 -Normen
-Normen
![\begin{eqnarray*}
\|f - g\|_{p,w} & := &
\left(\int\limits_a^b (w(t) \cdot |f(t) - g(t)|)^{p} dt \right)^{1/p}, \,
p \in [1,\infty), \\
\|f - g\|_{\infty,w} & := &
\max \, \{ w(x) \cdot |f(x) - g(x)|: x \in [a,b] \}.
\end{eqnarray*}](pic/f04_0405.gif)
Die Wahl der Gewichtung kann etwa auf Schätzungen der absoluten Genauigkeit der y-Werte - z.B. ausgedrückt durch Schätzungen der Streuung - beruhen. Die Gewichte werden dann in diesem Fall umgekehrt proportional zur Genauigkeitsschätzung gewählt.
* * *
Wenn bekannt ist, daß die relative Genauigkeit aller y-Werte gleich ist, d.h., wenn die absolute Genauigkeit aller y-Werte proportional zu y ist, dann können die Gewichte im Vektorfall folgendermaßen definiert werden:
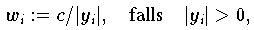
wobei c > 0 eine beliebige Konstante ist.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]