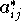unter den Konkurrenten in seiner Spalte wenigstens zu den
größeren gehört (zB. > 25%).Ist diese Bedingung
erfüllt, so wird das Element genommen, andernfalls
testet man das Nächste zur Verfügung stehende.
Aus der momentanen Besetzungsstruktur einer Matrix läßt sich durch Analyse feststellen, wieviele Leerstellen bei der Wahl eines bestimmten Elements zum Pivot-Element durch Auffüllung (,,Fill-in``) verlorengehen. Man versucht daher, das nächste Pivot-Element so zu wählen, daß beim nächsten Eliminationsdurchgang eine möglichst geringe Auffüllung stattfindet. Man nimmt daher alle Zeilen und Spalten als Kandidaten, die noch kein Pivot-Element geliefert haben. Diese Methode liefert zwar nicht das Optimum, aber immerhin eine sehr gute Annäherung an das globale Optimum.
Unkontrolliert darf man diese Strategie allerdings nicht anwenden, da man sonst die numerische Stabilität zerstören könnte .
Daher greift man zu einem Kompromiß: Man untersucht, ob das
ausgewählte Element
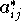unter den Konkurrenten in seiner Spalte wenigstens zu den
größeren gehört (zB. > 25%).Ist diese Bedingung
erfüllt, so wird das Element genommen, andernfalls
testet man das Nächste zur Verfügung stehende.
Damit bleibt die Gesamt-Auffüllung meist erträglich und die numerische Stabilität wird nicht verschlechtert.
An diesen Überlegungen erkennt man schon, das der Entwurf von Algorithmen für schwach besetzte Systeme offensichtlich ein bischen mehr Überlegungen und Hirnschmalz verlangt als dies bei mäßig vollbesetzten Matrizen der Fall ist.