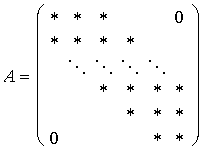
Sehr angenehm in der Verarbeitung sind Bandmatrizen (siehe auch ...), wenn wir Gauß-Elimination ohne Pivotsuche betreiben. Bei der Faktorisierung entstehen keine neuen Nicht-Null-Elemente außerhalb der Bandbreite. Allerdings erkaufen wir uns diese Eigenschaft mit der Gefahr der Instabilität.
| Gegeben sei eine Bandmatrix mit einer linken Bandbreite p und einer rechten Bandbreite q |
 |
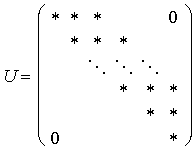
| Nach der LU-Faktorisierung ohne Pivotsuche erhalten wir die Matrizen |
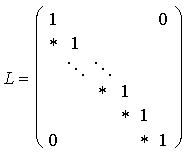
|
|
Dabei hat die Dreiecksmatrix L nun eine linke Bandbreite von p und U eine rechte Bandbreite von q. Erinnern wir uns nochmals, daß es zu Instabilitäten kommen kann, da wir keine Pivotsuche durchführen. Wenn wir allerdings eine Spaltenpivotsuche durchführen, so können in der Nebendiagonale der oberen Dreiecksmatrix neue Nicht-Null-Elemente entstehen. Von diesen wissen wir aber, daß sie nicht weiter als die Summe der rechten und linken Bandbreite von der Hauptdiagonale entfernt sind.
Betrachten wir dazu nochmals unsere Ausgangsmatrix A:
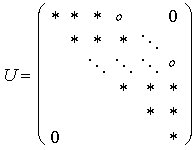
| Wir erhalten als Ergebnis der LU-Faktorisierung mit Spaltenpivotsuche eine Matrix U mit einer oberen Dreiecksmatrix, deren rechte Badbreite maximal p + q ist. An den mit o gekennzeichneten Stellen haben wir dabei die auffüllung. |
|