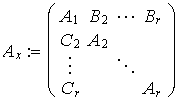
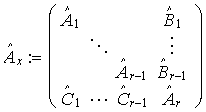
Um schwach besetzte Systeme effizient bearbeiten zu können, versucht man durch spezielle Speichertechniken die Operationen mit den Nullelementen der Matrix so weit wie möglich zu minimieren. Man speichert daher im Wesentlichen nur die Nicht-Null-Elemente und deren Position.
Wenn man nun die herkömmliche Gauß-Elimination benützen würde, so entstünden an Stellen, die vorher Null waren, neue Nicht-Null-Elemente. Da das Eintragen dieser Elemente sehr aufwendig ist, versuchen wir lieber gleich, das Entstehen neuer Elemente so gering wie möglich zu halten.
Wir werden daher unser Wissen über die Struktur einer Matrix nützen. So können wir in vorhinein feststellen, wo später Auffüllungen notwendig werden, und das gleich berücksichtigen.
Sehr oft läßt sich auch durch Umordnen das Entstehen von
neuen Nicht-Null-Elementen reduzieren. Wir betrachten zB. die
folgenden Blockpfeilmatrizen (blockarrowhead-matrices)
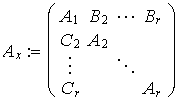
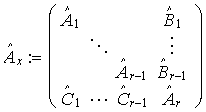
Durch einfache Umkehrung der Spalten- und Zeilenreihenfolge
können beide Matrizen ineinander übergeführt werden.
Wenden wir auf beide Matrizen die LU-Faktorisierung an,
so wird im ersten Fall fast die gesamte Matrix aufgefüllt,
im zweiten Fall findet aber keine
keine Auffüllung außerhalb der Blöcke
statt.