[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

Poisson-Matrix

Kleine Einführung in die Materie

Die Poisson-Differentialgleichung im zweidimensionalen Fall lautet

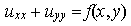
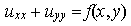
$u_{xx}+u_{yy}=f\left( x,y\right) $

Als Funktion haben wir gegeben:

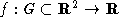
$f:G\subset \Re ^2\rightarrow \Re $

Zusätzlich haben wir noch die Randbedingung u für die gilt:

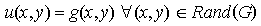
$u\left( x,y\right) =g\left( x,y\right) \ \forall \left( x,y\right) \in Rand\left( G\right) $

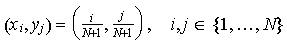
Rand(G) ist dabei der Rand des Gebietes, auf dem die Lösung u gesucht wird. Ist das Gebiet z.B. das Einheitsquadrat G:=[0,1]x[0,1] und wählt man dort eine äquidistante Schrittweite h:=1/(N+1) in x- und y-Richtung, so erhält man die folgenden Gitterpunkte im Inneren von G: $\left( x_i,y_j\right) =\left( \frac i{N+1},\frac j{N+1}\right) ,\quad i,j\in \left\{ 1,\ldots ,N\right\} $

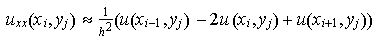
An diesen Stellen approximiert man die 2. partiellen Ableitungen von u(x,y) durch folgende Differenzenquotienten: $u_{xx}\left( x_i,y_j\right) \,\approx \frac 1{h^2}\left( u\left( x_{i-1},y_j\right) \,-2u\,\left( x_i,y_j\right) +u\left( x_{i+1},y_j\right) \right) $

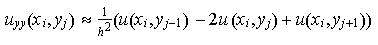
$u_{yy}\left( x_i,y_j\right) \,\approx \frac 1{h^2}\left( u\left( x_i,y_{j-1}\right) \,-2u\,\left( x_i,y_j\right) +u\left( x_i,y_{j+1}\right) \right) $

Nun die gewonnenen Näherungswerte in die Poisson-Gleichung einsetzen

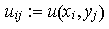(dabei ist $u_{ij}:=u\left( x_i,y_j\right) $ )

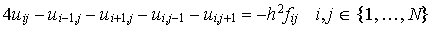
und man erhält die Gleichungen $4u_{ij}-u_{i-1,j}-u_{i+1,j}-u_{i,j-1}-u_{i,j+1}=-h^2f_{ij}\quad i,j\in \left\{ 1,\ldots ,N\right\} $

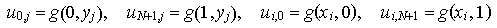
sowie am Rand von G $u_{0,j}=g\left( 0,y_j\right) ,\quad u_{N+1,j}=g\left( 1,y_j\right) ,\quad u_{i,0}=g\left( x_i,0\right) ,\quad u_{i,N+1}=g\left( x_i,1\right) $

Wie man sieht, erhält man ein (lineares) Gleichungssystem mit N*N Unbekannten und ebensovielen Gleichungen. Durch zeilenweise Numerierung der Gitterpunkte von 1 bis N*N und entsprechende Umordnung erhält man folgende Tridiagonalmatrix (die sogennante Poisson-Matrix)

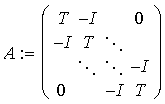
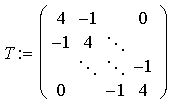
$A:=\left( \matrix T & -I & & 0 \\ -I & T & \ddots & \\ & \ddots & \ddots & -I \\ 0 & & -I & T\endmatrix \right) $ $T:=\left( \matrix 4 & -1 & & 0 \\ -1 & 4 & \ddots & \\ & \ddots & \ddots & -1 \\ 0 & & -1 & 4\endmatrix \right) $

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]