8.12.02 QR- Verfahren:

Eine Wesentlich weniger störungsanfällige Methode (im vergleich zu Normalgleichung) zur Lösung von L2-Ausgleichsproblemen beruht auf der sogenannten QR-Faktorisierung von A, wird also auf die Daten des ursprünglichen Problems angewendet.

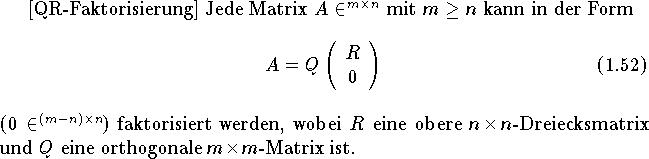
Wenn die Matrix A vollen Rang n hat, so ist die Dreiecksmatrix R nichtsingulär und die QR-Faktorisierung kann zur lösung des L2-ausgleichsproblems verwendet werden, da

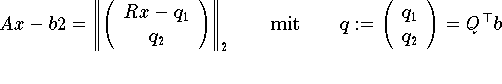
Gleichungssystems Rx = q1 ist. Es gilt

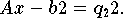
Wenn A nicht vollen Rang hat oder der Rang von A nicht bekannt ist, kann man eine QR- Faktorisierung mit Spalten-Pivotstrategie oder eine Singulärwertzerlegung durchführen. Die QR-Faktorisierung mit Spalten-Pivotstrategie ist im Fall m >= n gegeben durch

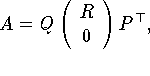
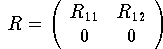
hat, wobei R₁₁ eine quadratische nichtsinguläre Dreiecksmatrix ist. Die sogenannte Basislösung des linearen Ausgleichsproblems erhält man durch QR -Faktorisierung mit Pivotstrategie. Durch Anwendung orthogonaler (unitärer) Transformationen kann R₁₂ eliminiert werden, und man erhält die vollständige orthogonale Faktorisierung, aus der man die Lösung mit minimaler Norm gewinnt.

[<] [globale Übersicht] [Kapitelübersicht] [Stichwortliste] [>]