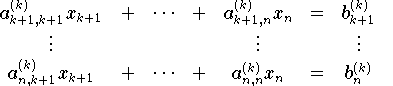
[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]

Bei der Ausführung des Eliminationalgorithmus muß man beachten, daß dessen Durchführung auf Hindernisse stoßen kann. Die verwendung der ersten Gleichung des nach k Schritten verbliebenen System

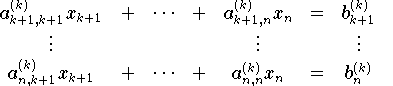
von n-k Gleichungen in den Unbekannten xk+1,...,xn zurElimination von X k+1in der (k+2)-ten.(k+3)-ten,...,n-ten Gleichung ist nur möglich, falls der Koeffizient a(k)k+1,k+1 von Null verschieden ist. Aber auch schon ein (relativ zu den anderen Koeffizienten)sehr kleiner Wert von a(k)k+1,k+1 ist nicht unbedenklich. Ein solcher Wert ist oft durch Auslöschung entstanden. Seine dementsprechend geringe relative Genauigkeit wirkt sich auf die ganze weitere Rechnung und den Ergebnisvektor störend aus.

  • Beispiel

    Diese Schwirigkeit läßt sich jedoch durch eine Modifikation des Algorithmischen Ablaufs umgehen: Da die Reihenfolge der Gleichung für die Lösung irrelevant ist ,bringt man einfach durch Vertauschung eine solche Gleichung in die (k+1)-te Zeile, bei der der Koeffizient von xk+1 den größten Absolutbetrag hat. Bei der rekursiven Überführung des Gleichungssystems in die Dreieckgestalt wird deshalb vor jedem Eliminationsschritt eine sogenante Pivotsuche durchgeführt: Beim (k+1)-ten Schritt wird in der ersten Spalte der Koeffizientenmatrix des verbleibenden Systems der betraggrößte Koeffizient gesucht. Die so gefundene Pivotzeile wird dann mit der ersten Zeile (=Gleichung) von ()vertauscht, sodaß im Nenner der bei der Elimination verwendeten Faktoren das bei der Pivotsuche bestimte Matrixelement steht. Dadurch haben alle Eliminationsfaktoren

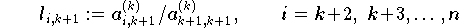
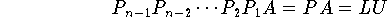
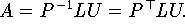
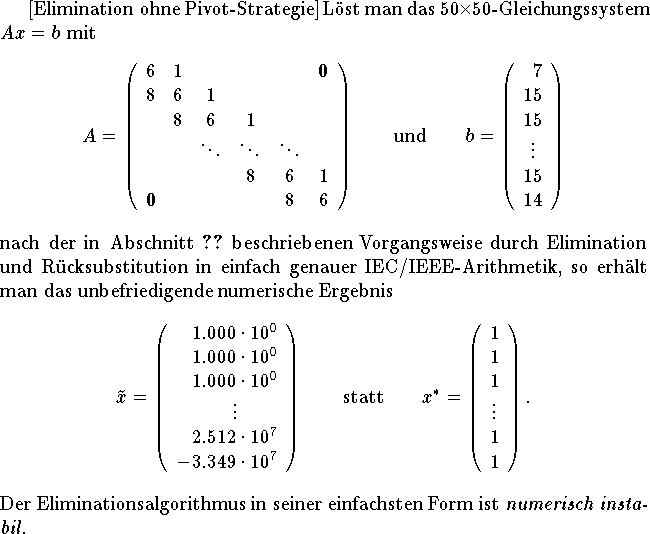
    einen Betrag <=1. Wenn man jede einzelne Zeilenvertauchung durch eine Permutationmatrix Pk ausdrükt, so sieht man, daß die Dreieckzerlegung

    von PA und nicht von (A) berchnet wird. Die Faktorisierung von (A) ist

    Man kann zeigen, daß die Zeilenvertauschungen ausschlaggebend für die Stabilität des Eleiminationsalgorithmus sind. Diese Algorithmische Technik wird als Spaltenpivotsuche bezeichnt.

    [<] [globale Übersicht] [Kapitelübersicht] [Stichwortliste] [>]