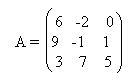[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]

  • 8.10.02 LU Zerlegung:

    Dem Eliminationvorgang, der aus dem ursprünglichen System schließlich das Dreiecks-System macht, entspricht eine Zerlegung der Matrix A

    deren Faktoren Dreiecksmatrizen sind.Man spricht daher auch von einer Dreieckszerlegung der Matrix A. L ist eine untere (lower) Dreiecksmatrix mit

    und U eine obere (upper) Dreiecksmatrix, die Koeffizientenmatrix des reduzierten Gleichungssystem :

    Die Enstehung der Matrix L hängt mit den Eliminationsschritten zusammen. Dem ersten Schritt, der den Übergang von dem ursprünglichen System zu dem Dreiecks-System bewirckt, entspricht die Matrizenmultiplikation M1A mit

    Das Dreiecks-System erhält man durch

    wobei die sogenante Gauß-Transformation Mk durch

    gegben sind. Jede Gaus-Transformation ist eine untere Dreiecksmatrix, deren Diagonalelement alle 1 sind. Dementsprechend hat auch die Produktmatrix M und deren Inverse M-1 diese Gestalt. Aus

    Auf der Basis der LU-Zerlegung von A ist die Lösung des Gleichungssystem Ax = b ein dreistufiger Vorgang:

    ZERLEGEN A=LU.

    LÖSEN Ly=b.

    LÖSEN Ux=y.

    Die Aufteilung in Faktorisierung und Auflösung hat noch den Vorteil, daß der erste, aufwendige Schritt nur einmal durchgefürt werden muß, falls mehrere Gleichungssysteme mit gleicher Koeffizientenmatrix, aber verschidenen rechten Seiten zu lösen sind.Diser Fall kommt in der Praxis recht häufig vor.

  • Bemerkung :Dieser Algorithmus funktioniert nur bei Matrizen ,die eine Inverse Matrix besitzen, sonst kann man das Gaußsche Eliminationsverfahren nicht einsetzen.

  • Pseudocode

    Pseudocode für die Zerlegung einer Matrix A in Zwei Matritzen L,U wobei

    A = LU. 
     FOR j:=1  TO n-1 DO

   FOR i:=j+1 TO n DO

     in A (Konstante * Zeile[j]) + Zeile[i] sodaß a[ij]=0;

     in U Zeile[i]:=(Konstante * Zeile[j]) + Zeile[i];
 
     in L aij:= inverse der konstante ;
     {Die Konstante kann man so wählen aij oder -aij} 
     END;

  • Beispiel

    Gesucht ist die LU-Zerlegung von der Matrix A.

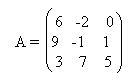  • Mittels Gaußscher Eliminationsverfahren bildet man die U Matrix,dabei merkt man sich den Multiplikator jeder Zeile. Um die Elimination leichter zu erhalten ,soltt die Elemente in der Hauptdiagonale durch Division oder Multiplikation auf 1 setzen .
  • Nun wird die Hauptdiagonale von L Matrix gebildet ,in dem man Anstelle von A[a11] das Inverse von dem Multiplikator ,das heißt wenn man das Element [a11]mit 1/6 multipliziert hat,um von 6 auf 1 zu kommen ,so setzt man in der L Matrix anstelle von [a11] das Inverse von 1/6 d.h 6.

  • Analog zu Schritt zwei ersetzt man jedes Element [aij] durch das Inverse des Zeilenmultiplikators(also das Inverse der Zahl, mit der man das Element aij Multipliziert hat um eine0 zu gewinnen.)

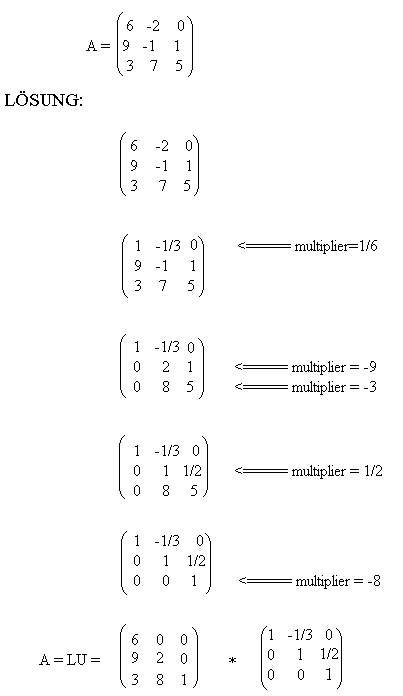
  • Somit hat man A in eine L und eine U Matrix ersetzt ,und es gilt A = LU.

    Die Ursprüngliche Matrix lautet:

    [<] [globale Übersicht] [Kapitelübersicht] [Stichwortliste] [>]