[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]

• 8.10.01 Eliminationsverfahren:

Die klassischen Verfahren zur numerischen Auflösung linearer Gleichungssysteme beruhen auf bereits in Abschnit5.7.1geschilderten Vorgangsweise:Da eine Linearkombination von Gleichung nichts an der Lösung des Gleichungssystems ändert,werden geeignete Linearkombinationen zur systematischen Elimination von unbekanten benützt. Durch Multiplikation der ersten Gleichung des Systems

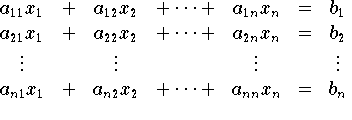
mit a_i1/a₁₁(a₁₁ ungleich 0)und Subtraktion dieser gleichung von der i-ten Gleichung fällt der Term mit x₁ in der entstehenden Gleichung weg. Man erhält so für i=2,3,...,n ein System von n-1 linearen Gleichungen

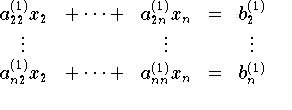
in den n-1 Unbekanten x₂,x₃,...,x_n mit

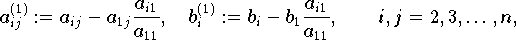
das zusammen mit der ersten, unveränderten Gleichung

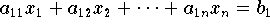
äquilent zum ursprunglichen System ist. Falls mit a_ii^(k) = 0 keine Sondersituation auftritt, Läßt sich dieses Verfahren rekursiv fortsetzen. Nach n-1 Rekursionsschritten ist das verbleibende System schliesslich auf eine gleichung in einer Unbekanten xn reduziert,und das äquivalente Gleichungssystem hat folgende Gestalt

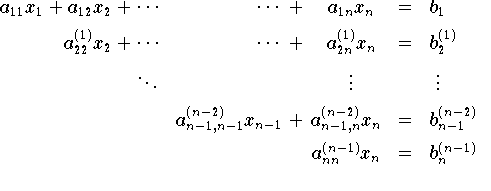
Die a_ii^(k) = 0 und b_i^(k) sind dieneuen, durch die Eliminationsrechnung entstehenden Koeffizinten bzw. Elemente der rechten Seite, wobei der obere Index k zum Ausdruk bringt , wie oft der Wert von a_ij bzw.b_ihöchstens verändert wurde. Ein Gleichungssystem von der Struktur heisst gestaffeltes System oder Dreiecks-System, die zugehörige Koeffizintenmatrix ist eine obere (oder rechte)Dreiecksmatrix. ein solches Gleichungssystem läßt sich durch Rücksubstitution rekursiv lösen, falls alle Diagonalkoeffizinten von Null verschieden sind. Die letzte Gleichung liefert

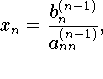
nach Einsetzen von xn in die vorletzte Gleichung liefert diese

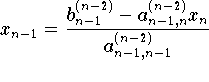
usw; schlißlich hat man die Lösungskomponenten x₂,...,x_n und erhält nach Einsetzen in die Erste Gleichung noch

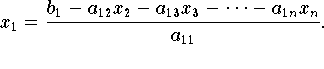
  FOR j:=1 TO n-1  do

   FOR i:=j+1 TO n  do

    (Konstante * Zeile[j])+Zeile[i] sodaß a[ij]=0;
    Zeile[i]:=(Konstante * Zeile[j])+Zeile[i];
    {Die Konstante könnte man so wählen aij-aij}
 end; 

Beispiel

Man hat das folgende Gleichungssystem zu lösen:-

                   -X2+X3 = 0
                -X1+X2+X3 = 1
                 X1+X2+X3 = 3.

Lösung:-

Man bildet die Matrix

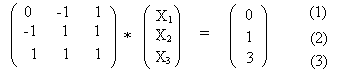
durch vertauschen zwischen 1. Und 2. Gleichung erhält man die Matrix :-

Dann addiert man die 1.Gleichung zur den 3. Gleichung :-

Dann, multipliziert man die 2.Gleichung mit 2 und addiert das Ergebnis zu 3. Gleichung, So erhält man

Somit ist 4X3 = 4 X3 = 1 ersetzt man den Wert von X3 in die 2.Gleichung so erhält man

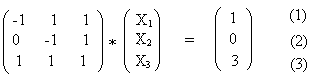
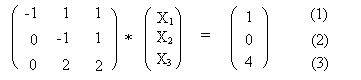
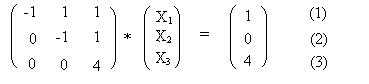
-1X2 + 1= 0, X2 = 1. Und ersetzt man den Wert von X3 und den Wert von X2 in die 1. Gleichung so erhält man -1X1 + 1 + 1 = 1 , X1 = 1.

---

[<] [globaleübersicht] [Kapitelübersicht] [Stichwortliste] [>]