[ < ] [
globale Übersicht ] [ Kapitelübersicht
] [ Stichwortsuche ] [
> ]
6.8.2 Anwendungen von Polynomsubsplines:
Schönbergsche Splineapproximation
Bisher wurde davon ausgegangen, daß die Teilungspunkte xi von Splinefunktionen
mit jenen Punkten, an denen die gegebene Funktion f interpoliert werden soll, zusammenfallen.
Da die Teilungspunkte gerade jene Punkte sind, an denen eine verringerte Glattheit der
Interpolationsfunktion auftritt, ist diese spezielle Wahl z.B. dann sinnvoll, wenn auch
die zu interpolierende Funktion an den Interpolationsknoten eine solchermaßen verringerte
mathematische Glattheit aufweist. Ist jedoch f an den Interpolationsknoten nicht mit einer
verringerten Glattheit behaftet, ist es möglich - und oft auch sinnvoll - die Teilungspunkte
xi von den Interpolationsknoten abweichend zu wählen.
Die Entkoppelung von Interpolationsknoten und Teilungspunkten kann insbesondere dazu benützt
werden, die Anzahl der Teilungspunkte so zu wählen, daß die Anzahl der linear
unabhängigen B-Splines mit der Anzahl der Interpolationsknoten übereinstimmt.
Dadurch entfällt die sonst notwendige, unter Umständen recht willkürliche
Annahme von zusätzlichen Randbedingungen. Interpolationsknoten und Teilungspunkte können
aber nicht gänzlich unabhängig voneinander gewählt werden; nicht für jede
Wahl der Teilungspunkte ist das Interpolationsproblem lösbar. Weiters hat die Wahl der
Teilungspunkte einen Einfluß auf die Approximationsgüte des Interpolationssplines.
Eine weitere Modifikation der Wahl der Teilungspunkte ist durch zusammenfallende Knoten
xi möglich. Wenn genau m Knoten xi zusammenfallen, z.B. an der
Stelle u, so bezeichnet man u als einen Knoten der Vielfachheit m. Für m=1 spricht man
von einem einfachen Knoten, für m=2 von einem doppelten Knoten usw. An einem Knoten der
Vielfachheit m ist die Splinefunktion s ebenso wie ihre ersten d-m Ableitungen stetig.
Für m=d ist s' an der Stelle u unstetig; für m=d+1 hat die Splinefunktion s eine Sprungstelle
bei x=u. Ein Zusammenfallen von mehr als d+1 Knoten ist nicht zulässig.
Durch die Wahl mehrfacher Knoten wird es insbesondere möglich, das Verhalten der
Splinefunktion an jenes der zu interpolierenden Funktion an Stellen mit verringerter Glattheit
anzupassen.
Interessante Anwendungen für B-Splines gibt es z.B. in der graphischen Datenverarbeitung.
So ist es etwa in CAD-Systemen sehr wichtig, dem Konstrukteur ein Werkzeug zur Verfügung
zu stellen, mit dessen Hilfe er in möglichst einfacher Weise verschiedene Kurven oder Flächen
nach seiner Vorstellung definieren kann. Eine häufig verwendete Methode besteht darin, daß
der Konstrukteur eine endliche Menge von Punkten vorgibt, die die Kurve festlegen.
Wichtig ist dabei weniger, daß die Kurve die vorgegebenen Punkte interpoliert, als vielmehr,
daß der Zusammenhang zwischen der Lage der Punkte und der sich ergebenden Kurvenform
für den Konstrukteur möglichst leicht und intuitiv verständlich ist. Gerade in dieser
Hinsicht erweist sich die Interpolation vorgegebener Punkte oft als nicht gut geeignet. Insbesondere
führen das meist unvermeidbare Überschwingen der Interpolationsfunktion und der globale
Einfluß, den Datenwerte in manchen Interpolationsverfahren haben, oft zu unerwarteten und
unerwünschten Kurvenverläufen.
In einer solchen Situation kann man auf die Methode der Schönbergschen Splineapproximation
zurückgreifen. Für eine auf dem Intervall [a,b] definierte Funktion f und eine Knotenfolge
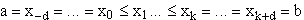
ist die Schönbergsche Splineapproximation g:=g(f) vom Grad d durch

definiert, wobei die Abszissen 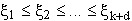 durch
durch
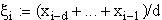 , i = 1,2,...,k+d,
, i = 1,2,...,k+d,
festgelegt sind. Die Funktion g weist folgende fundamentale Eigenschaften auf:
Satz: Auf dem Intervall [a,b] ist die Anzahl der Schnittpunkte der
Schönbergschen Splineapproximation g(f) mit einer beliebigen Geraden nicht
größer als die Anzahl der Schnittpunkte von f mit derselben Geraden.
Dieser zunächst recht abstrakt scheinende Satz läßt sich dann
anschaulich interpretieren, wenn man sich vor Augen hält, daß einer "Schwingung"
einer Funktion f stets ein Wendepunkt von f entspricht. Jeder Wendepunkt von f führt wiederum
zu einem Schnittpunkt von f mit bestimmten Geraden. Der obige Satz besagt daher, daß die
Schönbergsche Splineapproximation in keinem Fall stärker schwingen kann als die
Funktion f selbst. Als Spezialfälle dieses Sachverhaltes erhält man zunächst,
daß lineare Polynome 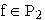 exakt reproduziert werden - g(f)=f -
und daß f >= 0 auch g(f) >= 0 nach sich zieht. Ferner ist für eine konvexe bzw. konkave
Funktion f auch die Schönbergsche Splineapproximation konvex bzw. konkav.
exakt reproduziert werden - g(f)=f -
und daß f >= 0 auch g(f) >= 0 nach sich zieht. Ferner ist für eine konvexe bzw. konkave
Funktion f auch die Schönbergsche Splineapproximation konvex bzw. konkav.
Eine weitere wichtige Eigenschaft von g(f) kann man direkt den obigen Definitionen entnehmen:
Ändert man einen Funktionswert 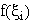 , dann wirkt sich dies auf
den Funktionsverlauf g(f) nicht global, sondern nur in d + 1 Teilintervallen
[xi-1,xi] aus. Umgekehrt wird der Funktionsverlauf von g(f) auf dem
Teilintervall [xi-1,xi] nur durch die d + 1 Funktionswerte
, dann wirkt sich dies auf
den Funktionsverlauf g(f) nicht global, sondern nur in d + 1 Teilintervallen
[xi-1,xi] aus. Umgekehrt wird der Funktionsverlauf von g(f) auf dem
Teilintervall [xi-1,xi] nur durch die d + 1 Funktionswerte
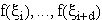 bestimmt. Die Schönbergsche Splineapproximation ist daher
ein lokales Approximationsverfahren.
bestimmt. Die Schönbergsche Splineapproximation ist daher
ein lokales Approximationsverfahren.
Weiters ist zu beachten, daß f im allgemeinen nur am Anfangspunkt a und am Endpunkt b, nicht
jedoch an den inneren Knoten x1,x2,...,xk-1 durch g(f)
interpoliert wird. Die Übereinstimmung g(xi) = f(xi) kann allerdings dadurch
erzwungen werden, daß xi als d-facher Knoten gewählt wird. Dennoch approximiert g(f)
bei hinreichend kleinen Knotenabständen xi - xi-1 jede gegebene Funktion
beliebig genau, soferne diese hinreichend differenzierbar ist. Es gilt nämlich für
![$f\in C^r\left[ x_o,x_k\right] $](pic/f08_0289.gif) und r >= 2
und r >= 2
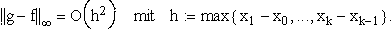
Will man eine Funktion g durch Angabe von k + d Punkten
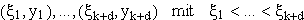
festlegen, so legt das bisher Gesagte folgende Vorgangsweise nahe: Die k + d Punkte werden als Werte einer
auf dem Intervall ![$\left[ \xi _1,\xi _{k+d}\right] $](pic/f08_0286.gif) definierten Funktion f aufgefaßt:
definierten Funktion f aufgefaßt:
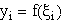 , i = 1,2,...,k+d.
, i = 1,2,...,k+d.
Die gesuchte Funktion g wird dann einfach als Schönbergsche Splineapproximation g(f) dieser Funktion f
festgelegt. Auf Grund der Approximationseigenschaft (siehe oben) ist dann zunächst (sofern die
Datenpunkte nicht zu weit voneinander entfernt sind) sichergestellt, daß die definierte Funktion g nie
stärker schwingt als eine beliebige andere Interpolationsfunktion.
Die praktische Durchführung dieser naheliegenden Vorgangsweise scheitert jedoch an der Berechnung
der Teilungspunkte x0,...,xk der Splinefunktion g. Im allgemeinen läßt
sich nämlich für eine vorgegebene Folge 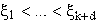 keine Knotenfolge
x-d = ... = x0 <= x1 <= ... <= xk = ... = xk+d so
angeben, daß die
keine Knotenfolge
x-d = ... = x0 <= x1 <= ... <= xk = ... = xk+d so
angeben, daß die 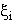 mit den definierten Stellen übereinstimmen.
mit den definierten Stellen übereinstimmen.
In der Praxis wird dieses Problem dadurch gelöst, daß die vorgegebenen Daten
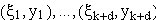 als Punkte einer ebenen Kurve (also nicht unbedingt einer Funktion)
interpretiert werden. Die Parameterdarstellung dieser Kurve wird im folgenden mit
als Punkte einer ebenen Kurve (also nicht unbedingt einer Funktion)
interpretiert werden. Die Parameterdarstellung dieser Kurve wird im folgenden mit
![$\left( f_1\left( \tau \right) ,f_2\left( \tau \right) \right) ,\quad \tau \in
\left[ a,b\right] $](pic/f08_0281.gif)
bezeichnet Man geht dann von einer Knotenfolge a = t-d = ... = t0 <= t1
<= ... <= tk+d = b des Parameterintervalls aus, bildet gemäß obiger Definition
die Folge 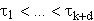 und interpretiert
und interpretiert 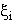 als
zum Parameterwert
als
zum Parameterwert 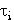 gehörig,
gehörig,
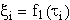 , i = 1,2,...,k+d.
, i = 1,2,...,k+d.
woraus sich unmittelbar ergibt, daß die yi ebenfalls den Parametern
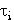 entsprechen:
entsprechen:
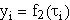 , i = 1,2,...,k+d.
, i = 1,2,...,k+d.
Auf Grund der speziellen Wahl der Punkte 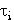 läßt sich die
zuvor beschriebene Methode auf beide Funktionen f1 und f2 anwenden, was zu
läßt sich die
zuvor beschriebene Methode auf beide Funktionen f1 und f2 anwenden, was zu
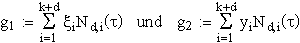
führt. Die durch die vorgegebenen Punkte definierte Kurve wird dann durch die Parameterdarstellung
(g1,g2) festgelegt. Diese Kurve erweist sich auf Grund der Monotonie von
g1 als Funktion g2(g1-1).
Man beachte, daß sich die hier beschriebene Vorgangsweise auch dann durchführen läßt,
wenn die angenommene Monotonie der Abszissen 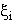 - durch die Werte y
i sollte ja eine eindeutige Funktion festgelegt werden - nicht zutrifft. Allerdings ist die
Funktion g1 bei nicht monoton wachsenden Werten
- durch die Werte y
i sollte ja eine eindeutige Funktion festgelegt werden - nicht zutrifft. Allerdings ist die
Funktion g1 bei nicht monoton wachsenden Werten 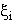 natürlich nicht mehr monoton, die resultierende Kurve (g1,g2)
läßt sich daher nicht mehr als Funktion auffassen. Dieser Anwendungsfall ist z.B. im
CAD-Bereich gegeben.
natürlich nicht mehr monoton, die resultierende Kurve (g1,g2)
läßt sich daher nicht mehr als Funktion auffassen. Dieser Anwendungsfall ist z.B. im
CAD-Bereich gegeben.
Für die Kurvenform ist neben der Anzahl der Teilungspunkte und des Splinegrades insbesondere
auch die Wahl der Parametrisierung - ausgedrückt durch die Wahl der Knotenpunkte ti
- entscheidend.
[ < ] [
globale Übersicht ] [ Kapitelübersicht
] [ Stichwortsuche ] [
> ]
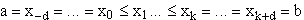
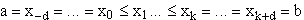

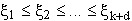 durch
durch
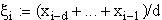 , i = 1,2,...,k+d,
, i = 1,2,...,k+d,
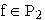 exakt reproduziert werden - g(f)=f -
und daß f >= 0 auch g(f) >= 0 nach sich zieht. Ferner ist für eine konvexe bzw. konkave
Funktion f auch die Schönbergsche Splineapproximation konvex bzw. konkav.
exakt reproduziert werden - g(f)=f -
und daß f >= 0 auch g(f) >= 0 nach sich zieht. Ferner ist für eine konvexe bzw. konkave
Funktion f auch die Schönbergsche Splineapproximation konvex bzw. konkav.
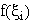 , dann wirkt sich dies auf
den Funktionsverlauf g(f) nicht global, sondern nur in d + 1 Teilintervallen
[xi-1,xi] aus. Umgekehrt wird der Funktionsverlauf von g(f) auf dem
Teilintervall [xi-1,xi] nur durch die d + 1 Funktionswerte
, dann wirkt sich dies auf
den Funktionsverlauf g(f) nicht global, sondern nur in d + 1 Teilintervallen
[xi-1,xi] aus. Umgekehrt wird der Funktionsverlauf von g(f) auf dem
Teilintervall [xi-1,xi] nur durch die d + 1 Funktionswerte
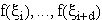 bestimmt. Die Schönbergsche Splineapproximation ist daher
ein lokales Approximationsverfahren.
bestimmt. Die Schönbergsche Splineapproximation ist daher
ein lokales Approximationsverfahren.
![$f\in C^r\left[ x_o,x_k\right] $](pic/f08_0289.gif) und r >= 2
und r >= 2
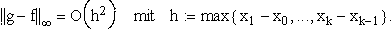
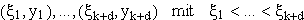
![$\left[ \xi _1,\xi _{k+d}\right] $](pic/f08_0286.gif) definierten Funktion f aufgefaßt:
definierten Funktion f aufgefaßt:
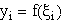 , i = 1,2,...,k+d.
, i = 1,2,...,k+d.
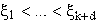 keine Knotenfolge
x-d = ... = x0 <= x1 <= ... <= xk = ... = xk+d so
angeben, daß die
keine Knotenfolge
x-d = ... = x0 <= x1 <= ... <= xk = ... = xk+d so
angeben, daß die 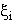 mit den definierten Stellen übereinstimmen.
mit den definierten Stellen übereinstimmen.
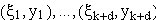 als Punkte einer ebenen Kurve (also nicht unbedingt einer Funktion)
interpretiert werden. Die Parameterdarstellung dieser Kurve wird im folgenden mit
als Punkte einer ebenen Kurve (also nicht unbedingt einer Funktion)
interpretiert werden. Die Parameterdarstellung dieser Kurve wird im folgenden mit
![$\left( f_1\left( \tau \right) ,f_2\left( \tau \right) \right) ,\quad \tau \in
\left[ a,b\right] $](pic/f08_0281.gif)
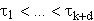 und interpretiert
und interpretiert 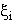 als
zum Parameterwert
als
zum Parameterwert 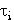 gehörig,
gehörig,
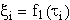 , i = 1,2,...,k+d.
, i = 1,2,...,k+d.
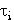 entsprechen:
entsprechen:
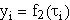 , i = 1,2,...,k+d.
, i = 1,2,...,k+d.
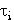 läßt sich die
zuvor beschriebene Methode auf beide Funktionen f1 und f2 anwenden, was zu
läßt sich die
zuvor beschriebene Methode auf beide Funktionen f1 und f2 anwenden, was zu
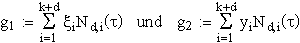
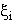 - durch die Werte y
i sollte ja eine eindeutige Funktion festgelegt werden - nicht zutrifft. Allerdings ist die
Funktion g1 bei nicht monoton wachsenden Werten
- durch die Werte y
i sollte ja eine eindeutige Funktion festgelegt werden - nicht zutrifft. Allerdings ist die
Funktion g1 bei nicht monoton wachsenden Werten 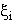 natürlich nicht mehr monoton, die resultierende Kurve (g1,g2)
läßt sich daher nicht mehr als Funktion auffassen. Dieser Anwendungsfall ist z.B. im
CAD-Bereich gegeben.
natürlich nicht mehr monoton, die resultierende Kurve (g1,g2)
läßt sich daher nicht mehr als Funktion auffassen. Dieser Anwendungsfall ist z.B. im
CAD-Bereich gegeben.