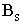[ < ] [globale Übersicht ] [ Kapitelübersicht] [ Stichwortsuche ] [> ]
[ Gerwin Szabo ]

6.8.2 Anwendungen von Polynomsubsplines:

B-Splines

Die Basis 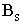Bs (Polynom_Splines) ist für praktische Anwendungen weniger geeignet. Die Gründe dafür sind :

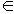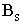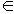  • Hoher Aufwand : Für x Element aus (X1-1,x1] haben d+i der Basisfunktionen in Bs einen von Null verschiedenen Wert. Die Auswertungvon s(x) kann daher für x Element aus (X1-1,x1] die Berechnung von bis zu d+k Summanden in der abgebrochenen Potenzdarstellung erfordern. Dieser maximale Rechenaufwand steigt selbst bei gleichbleibendem Polynomgrad d linear mit der Anzahl der Teilintervalle k an. Die Berechnung der Funktionswerte kann aber grundsätzlich mit einem von der Anzahl k der Teilintervalleunabhängigen Aufwand von O(d) Rechenoperationen bewerkstelligt werden,da s stückweise aus Polynomen vom Grad d zusammengesetzt ist. Der hohe Aufwand zur Berechnung der Funktionswerte fällt vorallem bei einer großen Anzahl von Teilintervallen auf.

  • Schlechte Kondition : Zusätzlich zum hohen Aufwand bei der Berechnung der Funktionswerte erweist sich die Bestimmung der Koeffizienten ai,j bei kleiner werdenden Abständen xi - xi-1 als schlecht konditioniert.

    • Definition

    Somit ist es zweckmäß:ig, zum Beispiel für Anwendungen im CAD-Bereich, Splinefunktionen nicht stückweise durch Teilpolynome Pin, sondern als Linearkombinationen von

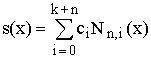
    $s(x)=\overset{k+n} \to{\underset{i=0}\to{\sum }}c_iN_{n,i}(x)$

    k+n linear unabhängigen B-Splines Nn,1......Nn,k+n darzustellen. Die Basisfunktion Nn,i - die normalisierten B-Splines - haben folgende Eigenschaften :

    $N_{n,i}=\left\{ \matrix >0\text{ }f\ddot ur\text{ }x\in \left( x_i,x_{i+n+1}\right) \\ =0\text{ }sonst\text{ }\endmatrix \right\} $

    d.h. die Nn,i nehmen nur lokal, auf n+1 benachbarten Teilintervallen von Null verschiedene Werte an. Für x 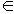Element aus [xi,xi+1] sind daher nur die Basisfunktionen Nn,i-n.....Nn,i zu berücksichtigen.

    $s(x)=\overset{i}\to{\underset{j=i-n}\to{\sum }}c_jN_{n,j}(x),$ $x\in \left[ x_i,x_{i+1}\right] $

    Wenn man nur einen Koeffizienten ci von s(x) verändert,dann wirkt sich dies nur auf den Funktionsverlauf von s in n Teilintervallen [xi,xi+1] aus; die Stetigkeits- und Differenzierungseigenschaften bleiben aber unverändert erhalten. Diese Eigenschaft der B-Spline-Darstellung ist z.B. bei CAD-Systemen sehr wichtig. Die normalisierten B-Splines Nn,i erhält man aus der folgenden von Cox und de Boor stammenden Rekursion :

    $N_{n,i}(x):=\left\{ \matrix 1\text{ }f\ddot ur\text{ }x\in \left[ x_i,x_{i+1}\right] \\ 0\text{ }sonst\endmatrix \right\} $ $N_{n,i}(x):=\frac{x-x_i}{x_{i+n}-x_i}N_{n-1,i}(x)+\frac{x_{i+n}-x}{x_{i+n+1}-x_{i+1}}N_{n-1,i+1}(x),$ $n=1,2,...$

    Eigenschaften von B-Splines

  • achsenunabhängig

  • mehrfache Knoten möglich

  • Interpolation von k-fachen Punkten

  • kein Überschwingen

  • lokales Interpolationsverfahren

  • Ecken innerhalb einer Kurve möglich

  • Aufwand steigt nur mit Länge der Kurve

  • ein jeder Punkt k-mal stetig differenzierbar

    • [ < ] [globale Übersicht ] [ Kapitelübersicht] [ Stichwortsuche ] [> ]