 Formel (7.6.1)
Formel (7.6.1)[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
Zunächst soll der Fehler eines Interpolationspolynoms Pd, das durch
 Formel (7.6.1)
Formel (7.6.1)

besitzt entsprechend der Interpolationsbedingung (7.6.1) an den Interpolationsknoten
x0 ,x1 ,...,xd Nullstellen; dazwischen können die Werte des Interpolationsfehlers
ed aber beliebig groß werden. Nur wenn zusätzliche Information
über f vorliegt, kann man auch dort Aussagen über die Größe
des Fehlers machen.
Wird eine Funktion f  Cd+1[a,b] an
den paarweise verschiedenen Knoten a <= x0 ,x1 , ...,xd <= b durch das Polynom Pd interpoliert,
so gibt es fü jedes x
Cd+1[a,b] an
den paarweise verschiedenen Knoten a <= x0 ,x1 , ...,xd <= b durch das Polynom Pd interpoliert,
so gibt es fü jedes x  [a ,b] eine Zahl
[a ,b] eine Zahl  aus dem kleinsten
Intervall, das alle xi und x enthält, sodaß sich der Fehler des Interpolationspolynoms
an der Stelle x durch
aus dem kleinsten
Intervall, das alle xi und x enthält, sodaß sich der Fehler des Interpolationspolynoms
an der Stelle x durch
 Formel (7.6.2)
Formel (7.6.2)
Beweis: Die Eigenschaft der Fehlerfunktion ed, an den Interpolationsknoten
x0 , ...,xd zu verschwinden, läßt sich durch
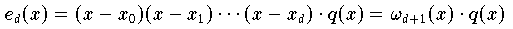 Formel (7.6.3)
Formel (7.6.3)
mit einer passenden Funktion q und dem
Knotenpolynom
wd+1 
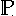 d+1
d+1
 [a ,b] mit
[a ,b] mit 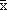
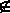 { x0 ,x1 , ...,xd } kann man mit wd+1 folgende Hilfsfunktion definieren:
{ x0 ,x1 , ...,xd } kann man mit wd+1 folgende Hilfsfunktion definieren: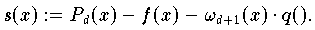
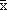 ) = 0 und s>(xi) = 0, i = 0,1,...,d
) = 0 und s>(xi) = 0, i = 0,1,...,d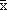 ,x0 ,x1 , ...,xd enthält,
hat die Funktion s also d+2 verschiedene Nullstellen. Da ausreichende
Differenzierbarkeit vorausgesetzt wurde, folgt aus dem Satz von Rolle, daß
s' in I mindestens d+1 Nullstellen besitzt. Weiteres Differenzieren
und neuerliche Anwendung des Satzes von Rolle zeigt , daß s'' mindestens
d Nullstellen in I besitzt. Dementsprechend hat schließlich s (d+1) mindestens eine Nullstelle in I, die im folgenden mit
,x0 ,x1 , ...,xd enthält,
hat die Funktion s also d+2 verschiedene Nullstellen. Da ausreichende
Differenzierbarkeit vorausgesetzt wurde, folgt aus dem Satz von Rolle, daß
s' in I mindestens d+1 Nullstellen besitzt. Weiteres Differenzieren
und neuerliche Anwendung des Satzes von Rolle zeigt , daß s'' mindestens
d Nullstellen in I besitzt. Dementsprechend hat schließlich s (d+1) mindestens eine Nullstelle in I, die im folgenden mit  bezeichnet wird.
bezeichnet wird.
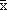 ) eine Konstante ist und
) eine Konstante ist und 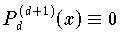
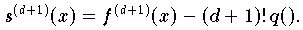
 von s (d+1) nach q(
von s (d+1) nach q(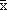 ) auflösen:
) auflösen:
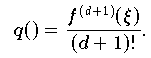
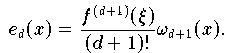
Mit einer Betragsschranke für die (d+1)-te Ableitung von f,
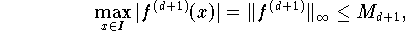
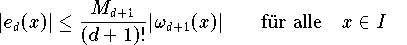 Formel (7.6.4)
Formel (7.6.4) 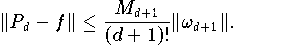 Formel (7.6.5).
Formel (7.6.5). ab. Die günstigste Knotenanordnung bezüglich der Fehlerabschätzung (7.6.5) erhält man, wenn
ab. Die günstigste Knotenanordnung bezüglich der Fehlerabschätzung (7.6.5) erhält man, wenn  so klein wie möglich ist. Für die
so klein wie möglich ist. Für die 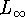 -Norm sind wegen Satz 9.3.1 (Tschebyscheff) die
Tschebyscheff-Nullstellen die optimalen Interpolationsknoten.
-Norm sind wegen Satz 9.3.1 (Tschebyscheff) die
Tschebyscheff-Nullstellen die optimalen Interpolationsknoten. C2[a ,b] durch einen Polygonzug, d.h. durch eine stückweise lineare Interpolationsfunktion auf einer
äquidistanten Knotenmenge (mit dem Stützstellenabstand h=(ba)/d) interpoliert wird, so
folgt aus
C2[a ,b] durch einen Polygonzug, d.h. durch eine stückweise lineare Interpolationsfunktion auf einer
äquidistanten Knotenmenge (mit dem Stützstellenabstand h=(ba)/d) interpoliert wird, so
folgt aus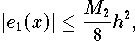

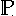 4 und approximiert sin(0.14) durch P4(0.14).
Mit
4 und approximiert sin(0.14) durch P4(0.14).
Mit![M_5 = \max \limits_{x \in [0, 0.4]} |\sin^{(5)}(x)| = \max \limits_I |\cos(x)| = 1](pic/f07_0639.gif)
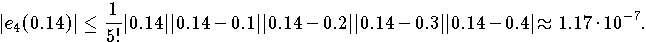 .
.

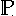 1, das durch die Punkte (x0 , f( x0)) und (x1 , f( x1)) geht,
ist durch
1, das durch die Punkte (x0 , f( x0)) und (x1 , f( x1)) geht,
ist durch 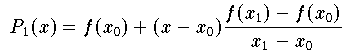
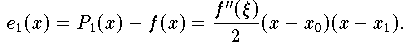 .
. [x0 , x1] und
[x0 , x1] und![M_2 := \max \{ |f''(x)|: x \in [x_0,x_1] \}](pic/f07_0645.gif)
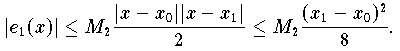 .
. .
.[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]