
Unter Homogenisierung versteht man das Generieren von analytischen (kontinuierlichen) Daten aus algebraischen (diskreten) Daten.
Die nach einer Diskretisierung (oder in Sonderfällen auch direkt) erhaltenen diskreten algebraischen Daten sind meist eine endliche Menge von Punkten, die bezüglich der unabhängigen Variablen (räumlich bzw. zeitlich) und bezüglich der Funktionswerte auf einem "Raster" liegen. Sie gestatten zunächst nur die Anwendung spezieller Verarbeitungsmethoden (Suchverfahren, Sortierverfahren etc.), da alle Methoden und Verfahren der Analysis, aber auch viele graphische Verfahren kontinuierlich definierte Funktionen voraussetzen, d.h. nur analytische Daten verarbeiten können. So ist z.B. eine Flächenberechnung nur möglich, wenn tatsächlich eine Fläche vorliegt; diskrete Punkte können keine Berandung einer Fläche bilden - hierfür ist ein Punktekontinuum erforderlich:

Aus den vorliegenden diskreten (algebraischen) Daten muß man in solchen Anwendungsfällen erst geeignete kontinuierliche (analytische) Daten generieren. Durch analytische Modellbildung - Homogenisierung - ist für die diskreten Daten ein kontinuierliches mathematisches Modell mit adäquater Beschreibungsgenauigkeit zu entwickeln.
Nach der Diskretisierung liegt Information über die zu modellierende (approximierende) Funktion f in Form einer endlichen Menge von Werten vor, z.B.
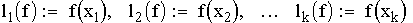
die zusammen mit den adaptiv oder nichtadaptiv gewählten Abtastpunkten {x1, x2, ..., xk} eine diskrete Punktmenge bilden:

Der Fall kontinuierlicher Information wurde damit auf den Fall diskreter Information zurückgeführt. Dementsprechend kann man auch bei der Funktionsapproximation die Methoden der diskreten Approximation, z.B. das Prinzip der Interpolation, verwenden, um die Parameter c1, c2, ..., cN der Approximationsfunktion g(x ; c1 c2, ..., cN) zu bestimmen.
Wenn man sich für einen Funktionstyp bzw. für eine Funktionenklasse G entschieden hat, aus der die Approximationsfunktion bestimmt werden soll, bleibt noch die Bestimmung der Parameteranzahl N und der konkreten Parameterwerte c1, c2, ..., cN offen. Man kann dazu nach einem Algorithmusschema vorgehen, bei dem eine Folge von Teilproblemen mit steigender Parameterzahl gelöst wird. Für jede Parameterzahl
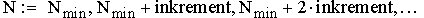
bestimmt man dabei nach einem vorher festgelegten Auswahlkriterium (Bestapproximation oder Interpolation, adaptive oder nichtadaptive Diskretisierung, Stützstellenverteilung etc.) eine Modellfunktion gN.
N := Nmin;
fehler := groesste_maschinenzahl;
do while fehler > T
end doberechne jene Funktion g(x ; c1, c2, ..., cN), die durch das Auswahlkriterium festgelegt ist; berechne eine Fehlerschätzung fehler; N := N + inkrement
Um das Terminieren eines Algorithmus nach diesem Schema garantieren zu können, muß die Konvergenz der Folge {gN} gegen die zu approximierende Funktion f sichergestellt sein. Die Effizienz des Approximationsalgorithmus wird vorwiegend durch die Konvergenzgeschwindigkeit dieser Folge bestimmt.
Die Implementierung eines konkreten Algorithmus nach diesem Schema muß auch auf Rundungsfehlereffekte Bedacht nehmen. Wird z.B. die Toleranz T bezüglich des aktuellen Rundungsfehlerniveaus zu klein gewählt, so terminiert der Algorithmus - ohne zusätzliche Abfragen - nicht. Auch die Wahl der Abtastpunkte kann sich auf das Resultat eines Homogenisierungsalgorithmus auswirken.