[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

[Thomas Stockinger]

6.8.2 Anwendungen von Polynomsubsplines

v-Splines

Von G.M.Nielson stammt eine Klasse von Interpolationsfunktionen, die stückweise aus kubischen Polynomen bestehen und für den parametrischen Fall (für ebene Kurven) die günstigen oszillationsdämpfenden Eigenschaften der Exponentialsplines besitzen, aber deren Nachteile vermeiden. Zur Definition dieser Funktionen wird der zweite Summand des Funktionals der Exponentialsplines diskretisiert:

$\dint\limits_a^b\left[ g^{\prime }(x)\right]^2dx+\dsum\limits_{i=0}^kv_i\left[ g^{\prime \prime }(x_i)\right] ^2,\quadv_i\geq 0,\quad i=0,1,...,k$

Die Funktionen, bei denen dieses Funktional minimal wird, besitzen im allgemeinen keine stetigen zweiten Ableitungen (sie würden sonst mit kubischen Splinefunktionen übereinstimmen); in den Randbedingungen kommen daher rechtsseitige und linksseitige zweite Ableitungen, g''( x+ ) bzw. g''( x- ) vor:

"Natürliche" Randbedingungen:

g''( a+ ) = v0g'( a )

g''( b- ) = vkg'( b )

Periodische Randbedingungen:

g( a ) = g( b )

g'( a ) = g'( b )

g''( a+ ) - g''( b- ) = ( v0 + vk ) g'( a )

Es zeigt sich, daß unter allen stetig differenzierbaren Interpolationsfunktionen mit quadratisch integrierbarer zweiter Ableitung, die entweder die natürlichen oder die periodischen Randbedingungen erfüllen, jene Funktion, für die der Wert des obigen Funktionals minimal wird, folgende Gestalt hat:

$s(x)=p+qx+\dsum\limits_{i=0}^{k-1}\alpha_i(x-x_i)_{+}^3+\dsum\limits_{i=0}^{k-1}\beta _i(x-x_i)_{+}^2$

Im Spezialfall v0 = v1 = ... = vk = 0 ist s die kubische Splinefunktion durch die Punkte ( xi, yi ), i = 0,1,...,k.

Für jede v-Splinefunktion - sowohl bei natürlichen als auch bei periodischen Randbedingungen - gilt die Ungleichung

$\dsum\limits_{i=0}^kv_i\left[ s^{\prime }(x_i)\right] ^2\leq M_1$

mit einer von den Parametern vi, i = 0,1,...,k unabhängigen Schranke M1.

Satz: Bei festgehaltenen vi und i 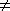$\neq $ k ist [s'( xi )]2 eine fallende Funktion von vi, und es gilt

$\lim \limits_{v_i\rightarrow \infty }s^{\prime }(x_i)=0$

Für wachsende Parameterwerte

$v_i\rightarrow \infty ,\quad i=0,1,...,k$

strebt also die v-Splinefunktion durch die Punkte ( xi, yi ), i = 0,1,...,k, nicht wie die Exponential-Splinefunktion gegen den interpolierenden Polygonzug, sondern gegen eine Funktion mit waagrechten Tangenten in den Knoten xi. Eine derartige Funktion ist daher als Ersatz der kubischen Splinefunktionen nicht unmittelbar geeignet. Erst durch den Übergang von einer Interpolationsfunktion zu einer interpolierenden ebenen Kurve können die vorteilhaften oszillationsdämpfenden Eigenschaften der v-Splinefunktion genutzt werden.

v-Spline Kurven

Ausgehend von einer Parametrisierung legt man durch die Punkte ( ti, xi ) und ( ti, yi ) je eine interpolierende v-Splinefunktion Xv(t) bzw. Yv(t). Je nach Art der Randbedingung kommt man so zu einer offenen oder geschlossenen ebenen Kurve durch die Datenpunkte ( xi, yi ), i = 0,1,...,k.

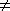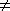Satz: Für Xv(t) $\neq $ 0 ist die Ableitung d2Yv / dXv2 an der Stelle t stetig. Analog ist d2Xv / dYv2 an der Stelle t stetig, wenn Xv(t) $\neq $ 0 gilt.

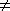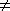Aus diesem Satz folgt sofort die für die Anwendung der v-Splinefunktionen wichtige Tatsache, daß für Xv(t) $\neq $ 0 oder Yv(t) $\neq $ 0 die Krümmung der Kurve (Xv(t), Yv(t)) für den Parameterwert t stetig ist.

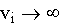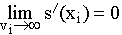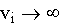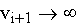Die stetige Krümmung geht im Grenzübergang $v_i\rightarrow \infty $ verloren. Wegen $\lim \limits_{v_i\rightarrow \infty }s^{\prime }(x_i)=0$ ist der Grenzfall für $v_i\rightarrow \infty $ und $v_{i+1}\rightarrow \infty $durch waagrechte Tangenten der Funktionen Xv und Yvan den Stellen xi und xi+1 gekennzeichnet. In diesem Fall ist die v-Splinekurve zwischen ( xi, yi ) und ( xi+1, yi+1 ) linear! 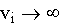Der Grenzübergang für alle $v_i\rightarrow \infty $ liefert also den interpolierenden Polygonzug. Durch ausreichend groß gewählte vi kann daher ein Überschwingen der Interpolationskurve vermieden werden.

Da man den Graph jeder Funktion auch als ebene Kurve auffassen kann, läßt sich die obige, auf parametrischer v-Spline-Interpolation beruhende Methode auch dort anwenden, wo man mit Interpolationsfunktionen zu keinen zufriedenstellenden Resultaten gelangt. Zu beachten ist allerdings, daß die interpolierende v-Spline-Kurve, außer im Extremfall des interpolierenden Polygonzuges, keine Funktion $s:\left[ a,b\right] \rightarrow \R$ sein muß, da einem x-Wert mehrere y-Werte entsprechen können.

Gewichtete v-Splinefunktionen

Die gewichteten v-Splinefunktionen sind jene stückweise kubischen Interpolationsfunktionen s(x), für die nicht das Funktional der v-Splines, sondern

$\dsum\limits_{i=0}^{k-1}\left( w_i\dint\limits_{t_i}^{t_{i+1}}\left[ g^{\prime\prime }(t)\right] ^2dt\right) +\dsum\limits_{i=0}^kv_i\left[ g^{\prime}(t_i)\right] ^2\quad mit\,allen\quad w_i,v_i\geq 0$

minimal ist. Zusätzlich zu 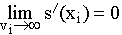$\lim \limits_{v_i\rightarrow \infty }s^{\prime }(x_i)=0$ gilt für diese Splinefunktionen auch

$\lim \limits_{w_i\rightarrow \infty }s^{\prime \prime }(t)=0\quad f\ddot ur\,alle\quad t\in \left[ t_i,t_{i+1}\right) $

Dem Anwender stehen damit zwei Parametervektoren v und w zur Verfügung, mit denen er die Gestalt der Interpolationsfunktion beeinflussen kann:

Der Einfluß dieser Parameter auf die Gestalt ebener v-Splinekurven wird in den Abbildungen und gezeigt:

Gewichtete v-Splinekurven mit v = (0,0,0,0,0,0), w = (10,1,20,1,10)

Gewichtete v-Splinekurven mit v = (1,1,40,40,1,1), w = (1,1,1,1,1)

Praktische Anwendungen gewichteter v-Splinefunktionen findet man vor allem im CAD-Bereich.

Berechnung von v-Splines

Soll die gesuchte v-Splinefunktion die natürlichen Randbedingungen

v0s'( a ) - s''( a+ ) = 0,

vks'( b ) - s''( b- ) = 0

erfüllen, so erhält man für die k+1 Unbekannten ein lineares Gleichungssystem mit Tridiagonalmatrix:

$\left[ \matrix b_0 & c_0 & & & 0 \\ a_1 & b_1 & c_1 & & \\ & a_2 & \ddots & \ddots & \\ & & \ddots & b_{k-1} & c_{k-1} \\ 0 & & & a_k & b_k\endmatrix \right] \left[ \matrix s_0^{\prime } \\ s_1^{\prime } \\ \vdots \\ s_{k-1}^{\prime } \\ s_k^{\prime }\endmatrix \right] =\left[ \matrix r_0 \\ r_1 \\ \vdots \\ r_{k-1} \\ r_k\endmatrix \right] $

Für den Fall y1 = yk kann man eine periodische v-Splinefunktion mit s1' = sk' berechnen. In diesem Fall erhält man das folgende lineare Gleichungssystem für die k Unbekannten s1', s2', ..., sk' :

$\left[ \matrix b_1 & c_1 & & & a_1 \\ a_2 & b_2 & c_2 & & \\ & a_3 & \ddots & \ddots & \\ & & \ddots & b_{k-1} & c_{k-1} \\ c_k & & & a_k & b_k\endmatrix \right] \left[ \matrix s_1^{\prime } \\ s_2^{\prime } \\ \vdots \\ s_{k-1}^{\prime } \\ s_k^{\prime }\endmatrix \right] =\left[ \matrix r_1 \\ r_2 \\ \vdots \\ r_{k-1} \\ r_k\endmatrix \right] $

Die beiden Koeffizientenmatrizen für die Berechnung der natürlichen und periodischen v-Splinefunktionen sind tridiagonal bzw. zyklisch tridiagonal und positiv definit. Zur Auflösung der Gleichungssysteme kann man daher den Gaußschen Eliminationsalgorithmus, modifiziert für (zyklisch) tridiagonale Matrizen, anwenden, der in diesem Fall auch ohne Pivotsuche numerisch stabil ist.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]