Mathematica

Wolfram Research, Champaign/ Illinois, USA

• Diese Software ist auch über den Campus Software Service der TU Wien erhältlich.
• Macintoshversion (Klicken Sie hier zum downloaden der Demo)
• UNIX-Version (Klicken Sie hier zum downloaden der Demo)
• Windowsversion (Klicken Sie hier zum downloaden der Demo)

Im Gegensatz zu Macsyma und Maple ist Mathematica nicht im universitären Bereich zur Welt gekommen, wohl aber liegen seine Wurzeln hier. Prof. Dr. Stefan Wolfram gründete für Mathematica seine Firma Wolfram Research.

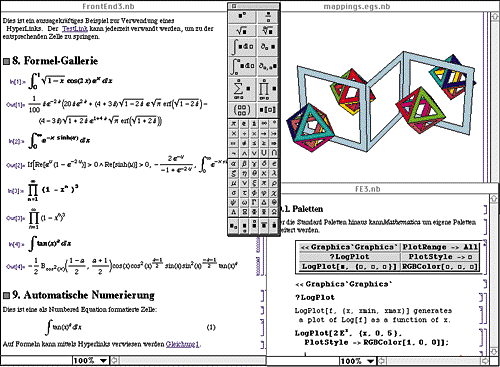
Mathematica ist ein interaktives, grafikorientiertes Mathematiksystem mit integrierter Hochsprache, das strukturiert prozedural oder regelbasiert programmiert wird. Über 850 integrierte Funktionen erlauben den schnellen Umgang mit der Mathematik. Lösungen werden exakt numerisch oder symbolisch angegeben. Auf diese Weise können auch komplexe Differentialgleichungen über numerische Näherung schrittweise gelöst werden. Erstellen Sie ein Rechenmodell mit Parametern und Ihr PC berechnet Ihnen alle möglichen Lösungen. Die hardwareoptimierten Grafikroutinen befähigen Mathematica Kontourplots zu generieren sowie 2D und 3D Darstellungen in Schwarz und Weiß sowie in Farbe.

Das Computer-Algebra-System Mathematica vereinigt symbolisches und numerisches Rechnen, Grafik, Animation, Listenverarbeitung und strukturierte Dokumentation mit einer mächtigen Programmiersprache. Mathematica befähigt den Anwender, die Tiefen der Mathematik auszuschöpfen, zu visualisieren und zu lösen ohne Papier und Bleistift, Taschenrechner oder komplexe Software. Durch die wahlfreie Genauigkeit und die Möglichkeit zur Matrixmanipulation, unterstützt Mathematica den Anwender ideal als interaktives Kalkulationswerkzeug und als Hochsprachen-Programmierumgebung. Es erlaubt Formeln direkt in algebraischer Form einzugeben und zu manipulieren. Darüberhinaus bietet Mathematica erweiterte Möglichkeiten zur symbolischen Gleichungslösung, Integration, Differentiation und Auflösung Gleichungen höherer Ordnung an. Die hardwareoptimierten Grafikroutinen befähigen Mathematica, Konturen zu generieren sowie 2- und 3-dimensionale Plots in Schwarz und Weiß sowie in Farbe auszugeben.

Numerische Berechnung

Mathematica arbeitet mit Zahlen arbiträrer (nach Ermessen, willkürlicher) Größe und Genauigkeit. Hierdurch erhält der Anwender vollständige Kontrolle über numerische Rundungsfehler. Dies erlaubt eine Vielzahl von Berechnungen mit sowohl theoretischem als auch praktischem Anspruch, die mit normalen wissenschaftlichen Taschenrechnern oder Standardprogrammiersprachen nicht möglich wären.

Mathematica's wahlfreie numerische Genauigkeit ermöglicht ein breites Anwendungsfeld an mathematischen Funktionen: trigonometrische und Exponentialfunktionen, Bessel-Funktionen, hypergeometrische Funktionen, elliptische Integrale und vieles mehr. Mathematica enthält natürlich auch effiziente numerische Algorithmen für die Matrizenrechnung, die numerische Integration und numerische Fähigkeiten zum Auflösen von Gleichungen.

Symbolische Berechnung

Neben numerischer Berechnung kann Mathematica auch mit algebraischen Formeln arbeiten. In Mathematica implementiert wurden alle Standardoperationssymbole der Algebra und Berechnung, einschließlich Integration, Differentiation und Polynomberechnung. Die Möglichkeit zur Manipulation und Ableitung exakter algebraischer Formeln befähigt den Anwender dazu, eine breite Palette von Berechnungen zu automatisieren, welche bisher nur per Hand erledigt werden konnten. Der Anwender von Mathematica kann sich explizit Formeln als Gleichungslösung anzeigen lassen; dies ist manchmal für das Verständnis der kompletten Struktur einer Lösung einfacher als numerische Resultate.

Graphische Berechnung

Das dritte Element von Mathematica ist die Grafik. Mathematica ermöglicht, Funktionen und Daten zweidimensional und dreidimensional, in Farbe oder Schwarz und Weiß darzustellen. Es realisiert anwendungsgerechte Visualisierung der Ergebnisse. Mathematica erzeugt ebenfalls dreidimensionale Farbbilder symbolischer Beschreibungen arbiträrer geometrischer Objekte. Zum Beispiel können Mathematica's Fähigkeiten zur symbolischen und numerischen Berechnungen verwendet werden, um eine Liste von Ansichten eines komplexen Polyhedrons zu erzeugen. Hieraus läßt sich über Mathematica's Grafikfähigkeiten ein dreidimensionales Bild erstellen.

Die meisten Mathematica Versionen unterstützen grafische Animation. Der Anwender erblickt zum ersten Mal eine dynamische Simulation oder die Veränderungen der Grafik bei Variation einer oder mehrerer Parameter.

Mathematica verwendet POSTSCRIPT für jede grafische Ausgabe. Diese größen- und auflösungsunabhängige Seitenbeschreibungssprache produziert auf Medien wie Computerbildschirmen, Laserdruckern, Photosetzmaschinen und anderen Ausgabegeräten Reports in Präsentationsqualität, Farbnegative für Bücher und Zeitschriften oder sogar riesige Poster. Mathematica speichert auch im Encapsulated POSTSCRIPT Format, sodaß Grafiken leicht in Dokumente anderer Programme eingefügt werden können, z.B. in Desktop Publishing Programme.

Programmierung

Mit den über 860 eingebauten Funktionen stellt Mathematica eine mächtige Programmiersprache dar, welche durch eigene Funktionen erweitert werden kann. Die Mathematica Sprache unterstützt verschiedene Programmierformen, wie die strukturierte prozedurale Programmierweise im Stile von C oder PASCAL und die funktionale Programmierung im Stile von APL. Seitdem die große Mehrheit der Algorithmen in der Mathematik dazu da sind, Instruktionen aus einer Gleichungsform in eine andere zu transformieren, erlaubt Mathematica regelbasiertes Programmieren. Hierdurch ist es möglich, Umwandlungsregeln für mathematische Ausdrücke zu spezifizieren. Jede Regel hat Bezug auf ein Modell und agiert als Ausdruck, der das Modell abbildet. Die meisten Regeln können durch direkte Umsetzung der Formeln aus Büchern konstruiert werden. Regeln können einen Namen erhalten und bei Bedarf aktiviert werden oder in einer globalen Regelbasis so implementiert sein, daß sie immer verfügbar sind.

Die Programmiersprache in Mathematica ist eine Hochsprache, die den Anwender in die Lage versetzt, komplexe Programme zu erstellen, die auf einfachen Funktionen basieren, welche wiederum direkt auf die primitiven Operationen in Mathematica selbst zugreifen. Viele solcher Programme sind in Form von Mathematica-Paketen verfügbar. Diese Pakete wurden von Mathematica Anwendern und Verkäufern über die Jahre hinweg erstellt und sind den verschiedensten Anwendungen angepaßt.

Systemarchitektur, Portabilität

Mathematica besteht aus zwei Teilen: dem Kernel, welcher die mathematischen Berechnungen vollzieht und die Programme ausführt sowie einem "Front End", das die Schnittstelle zum Anwender ist.

Der Kernel arbeitet auf jeder Computerplattform gleich. Aus diesem Aufbaukonzept resultiert, daß alle Softwarepakete, die mit Mathematica entwickelt wurden, auf dieser Computerplattform austauschbar sind. Andererseits ist das "Front End" so konstruiert, daß es die jeweiligen Möglichkeiten des Computers voll ausnutzt.

Das "Front End" und der Kernel brauchen nicht auf demselben Computer zu laufen. Alle Versionen sind untereinander kompatibel. So kann das "Front End" auf einem Computer laufen und über Modem mit einem anderen Computer kommunizieren, auf welchem der Kernel installiert ist. Dies ermöglicht Anwendern den Zugriff auf die Geschwindigkeit von Supercomputern mit dem gewohnten Präsentationsstil eines PCs.

Mathematica's Schnittstelle zu anderen Systemen

Mathematica bietet drei Möglichkeiten, um den Datenaustausch zu externen Programmen einfach und glatt zu gestalten.

Am einfachsten funktioniert dies über den Standard ASCII-Format. Mathematica liest z.B. numerische Daten, wie sie Tabellenkalkulations- und Datenbankprogramme produzieren. Grafiken können in den Dateiformaten von Desktop Publishing Systemen wie Adobe Illustrator, Aldus Pagemaker oder Animationspakete wie Video Works exportiert werden. Spezielle "Print Forms" lassen sich definieren, um symbolische oder numerische Ergebnisse zu exportieren, die in C oder FORTRAN implementiert werden können. Auch die Ausgabe in der Schriftsetzersprache TeX ist möglich.

Sollten Sie über ein Multitasking-System verfügen, welches interdisziplinäre Kommunikation ermöglicht, kann Mathematica Daten in Echtzeit übertragen (in UNIX ist dies durch Pipes realisiert). Mathematica bietet hierbei auch die Möglichkeit, Daten zu empfangen, z.B. von einem Labormeßinstrument oder einer Programmiersprache. Solche Programme können von Mathematica ablaufen oder selbständig mit dem Kernel in Verbindung treten.

Letztendlich bietet Wolfram Researchs registrierten Mathematica Entwicklern die Spezifikationen des internen Kommunikationsprotokolls MathTalk an, über das das "Front End" mit dem Kernel kommuniziert. Dies erlaubt es, eigene Programme zu entwickeln, die das Mathematica "Front End" ersetzen.

Internes

Wolfram Research entwickelte den Code des Kernels von Mathematica in einer objektorientierten Erweiterung von C. Der Code umfaßt nahezu 150.000 Zeilen. Wobei sich der Code nahezu gleichmäßig auf die einzelnen Bereiche in Mathematica verteilt. Die "Front End's" für Mathematica auf dem Macintosh und dem NeXT sind jeweils mehr als 50.000 Zeilen lang.

Die Portabilität von Mathematica zeigt sich in den über ein Dutzend verschiedenen Versionen für unterschiedliche Hardwarearchitekturen. Die hauptsächliche Einschränkung ist, daß nahezu 6 MB adressierbarer Speicher zur Verfügung stehen sollte. Für UNIX Workstations stellt dies keine Einschränkung dar, jedoch für den Macintosh bedeutet dies, daß entweder genügend physikalischer Speicher bereitgestellt werden muß oder ein virtuelles Speichermanagement unterstützt wird. Die Mathematica Version für den 386 MS-DOS Computer benötigt nur annähernd 4 MB physikalischen Speicher, da ein virtuelles Speichermanagementsystem eingebunden ist.

Vergleiche

Wie jedes intellektuelle Produkt hat auch Mathematica ein Vorleben. Als Programmierumgebung steht Mathematica auf einer höheren Sprachebene wie C oder FORTRAN, da sie symbolisch und interaktiv vorgehen kann. In seiner interaktiven Arbeitsweise ist Mathematica ebenso einfach aufgebaut wie BASIC, bei weitem aber leistungsfähiger. Im Bereich der numerischen Berechnung baut Mathematica auf Systeme wie APL und MatLab, mit jedoch stark erweiterten hochentwickelten Fähigkeiten, wie der frei wählbaren arithmetischen Genauigkeit. Gleichungslöser, wie TK!Solver und Eureka, beinhalten nur eine Handvoll der numerischen Funktionen von Mathematica. Im Bereich der symbolischen Manipulation stehen algebraische Berechnungssysteme, wie Macsyma, Maple, Reduce und SMP (ein früheres Produkt von Stephan Wolfram), am nächsten zu Mathematica. Diese Systeme weisen einige der Fähigkeiten von Mathematica auf, haben jedoch Mängel in ihrer allgemeinen Anwendbarkeit oder Programmierbarkeit. Einzigartig erscheint Mathematica in bezug auf die grafischen Möglichkeiten, vor allem durch die vollständige Integration dreidimensionaler Oberflächengrafiken in auflösungsunabhängigem POSTSCRIPT.

Durch die wahlfreie Genauigkeit und die Möglichkeit zur Matrixmanipulation, unterstützt Mathematica den Anwender ideal als interaktives Kalkulationswerkzeug und als Hochsprachen-Programmierumgebung. Die hardwareoptimierten Grafikroutinen befähigen Mathematica, Konturen zu generieren sowie 2- und 3-dimensionale Plots in schwarz-weiß sowie in Farbe auszugeben. Die Mathematica Benutzerschnittstelle, das sogenannte FrontEnd, besticht durch seinen hierarchischen Aufbau und die vielseitige Handhabung. Es erlaubt, Formeln direkt in algebraischer Form einzugeben und zu manipulieren. Darüberhinaus bietet Ihnen Mathematica erweiterte Möglichkeiten zur symbolischen Gleichungslösung, Integration, Differentiation und Auflösung von Gleichungen höherer Ordnung an. In der neuen Version 3 wurden Kernel und FrontEnd grundlegend verbessert. Mathematica stellt Ausdrücke als mathematische Formeln dar, einschließlich aller mathematischen Symbole und der griechischen Buchstaben; Eingaben können mit den Symbolpaletten per Mausklick erzeugt werden. Hinter diesen optischen Highlights verbirgt sich jedoch weitaus mehr als auf den ersten Blick ersichtlich. Wolfram Research ist es gelungen, die komplexe Struktur mathematischer Formeln auf die Mathematica Syntax abzubilden.

Programmierschnittstellen:

TeX, C, FORTRAN, MathLink

Datenimport/export :

ASCII, Binär (weitere durch Einbindung von FLT-Dateien)

Grafikimport/export :

BitMap (BMP), Device Independent Bitmap (DIB), Macpaint (MAC), Postscript (PS, EPS), Windows Metafile (WMF), Tagged Image File Format (TIFF), Adobe Illustrator File (AL), Wave (WAV)

Für eine aktuelle Übersicht, auf welchen Plattformen Mathematica-Versionen laufen, wählen sie bitte den Mathematica-Link auf der Homepage des Herstellers!

• Auch die Uni Frankfurt bietet aktuelle Informationen unter http://www.uni-frankfurt.de/~stst/mathe.html.
• Mathematica Applications Library: In der Programmiersprache von Mathematica geschriebene Zusatzpakete für diverse Anwendungsgebiete wie z.B. Finanz
  
  

  ---