Anzahl der Gleitpunktzahlen

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

4.5.3 Absolute Abstände der Gleitpunktzahlen

In diesem Abschnitt werden wir die Abstände der einzelnen Zahlen aus IF genauer betrachten, unter anderenm werden wir klären welchen Abstand die Zahlen zueinander haben.Umso größer der Abstand der Gleitkommazahlen ist desto größer wird auch der Rundungsfehler, wenn man eine reelle Zahl in einm Gleitpunktzahlensystem darstellen muß.

Nimmt man den Exponenten $e\in [e_{\min },e_{\max }]$ als fest an,so ist die

kleinste Mantisse durch die Ziffern $d_{1}=1,d_{2}=...=d_{p}=0$

und die größte Mantisse durch die Ziffern $d_{1}=d_{2}=...=d_{p}=\delta :=b-1$ festgelegt.

Bei einem festen Exponenten e durchläuft die Mantisse alle Werte von M_min bis M_max. Die nächst höhere Zahl von der Zahl x₁ mit dem Exponenten e=e₁ und M=M_max ist x₂ mit e=e₁+1 und M=M_min, wobei

$M_{\min }=0.100...00_{b}=b^{-1}$ und

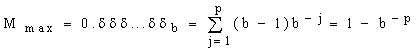$$M_{\max }=0.\delta \delta \delta ...\delta \delta$ .

Der Abstand zur nächsthöheren Zahl bei festem e beträgt b^-p .Dieser Abstand wird auch als Grundinkrement bezeichnet,es entspricht dem Wert einer Einheit der letzten Stelle der Mantisse,wird oft auch als ulp (unit of last position) bezeichnet. Als Abkürzung verwenden wir hier : u := 1 ulp = b^-p.

Die benachbarten Zahlen aus IF_N haben in einem Intervall [be,be+1], also bei festem Exponenten,einen konstanten Abstand von $\Delta x=b^{e-p}=u*b^e$ . Jedes Intervall in einem gegebenen Gleitpunksystem ist durch seine konstante, absolute Dichte charakterisiert. Insgesamt gibt es in jedem Zahlensystem e_max - e_min Intervalle, jedes mit seiner eigenen charakteristischen Dichte.

Beim Übergang zu einem nächstgrößerem Exponenten nimmt der Abstand der Zahlen in diesem Intervall um ein b-faches zu, im Gegensatz dazu nimmt aber die Dichte in diesem Intervall um das b-fache ab.Gegensätzliches passiert beim Übergang zum nächstkleinerem Exponenten. Hier nimmt der Abstand um ein b-faches ab und die absolute Dichte steigt um das b-fache an.

Übergang von e zu e+1:
Abstand der Zahlen nimmt um den Faktor b zu.
Absolute Dichte nimmt um den Faktor b ab.

Übergang von e+1 zu e:
Abstand der Zahlen nimmt um den Faktor b ab.
Absolute Dichte nimmt um den Faktor b zu.

Lücke um die Zahl Null

Der Bereich um die Zahl Null ist für die Numerische Mathematik ein wichtiger Bereich.Leider, bedingt durch die Normalisierung der Gleitpunktzahlen, überdecken die Zahlen aus IF_N den Bereich um die Zahl Null nicht ausreichend, d.h es entsteht eine Lücke um die Zahl Null.

denorm:= false:
In diesem Falle, wenn denorm = false, gibt es im Intervall [0,x_min] nur zwei Zahlen, nämlich die Grenzen selbst.

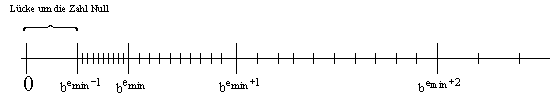
denorm := true:
Im Falle denorm = true wird das Intevall (0,x_min) mit bp-1-1 denormalisierten Zahlen gleichmäßig überdeckt. Sie besitzen den konstanten Abstand .

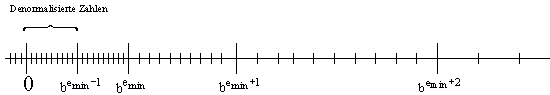
Die kleinste denormalisierte positive Zahl ist $x_{\min }:=\min \{x\in IF_{D}:x>0\}=u*b^{e_{\min }}=b^{e_{\min }-p}$ liegt wesentlich näherbei Null als die kleinste normalisierte Zahl x_min. Die negativen Zahlen ergeben sich wieder durch Spiegelung der positiven Zahlen um den Nullpunkt.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]