Gleitpunkt - Zahlensysteme

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

3.4.3 Gleitpunkt-Zahlensysteme:

Um den Nachteil der Festpunkt-Codierung zu vermeiden, wählt man einen Skalierungsparameter e $\in$ Z, der veränderlich (nicht fix) ist. Der Wert von e wird bei der Codierung angegeben. Die Gleitpunktzahlen werden in 3 Teilen dargestellt: Vorzeichen v, Exponent e und Mantisse M.

Terminologie:
Gleitpunktzahlen:In der Numerischen Datenverarbeitung wird meist von Gleitpunktzahlen (floating point numbers) und nicht von Gleitkommazahlen gesprochen. Diese Konvention steht nicht nur mit dem Dezimalpunkt, wie er in den englischsprachigen Ländern üblich ist, in Verbindung. Das Komma wird in den meisten Programmiersprachen als Trennzeichen für zwei lexikalische Elemente verwendet, sodaß z. B. die Zeichenkette 12, 25 demgemäß zwei ganze Zahlen, nämlich 12 und 25 bezeichnet, während 12.25 die (rationale) Zahl 49/4 symbolisiert.

Beispiel:

IEC/IEEE-Gleitpunktzahlen:In der Norm IEC 559:1989 für binäre Gleitpunkt-Arithmetiken werden zwei Grundformate spezifiziert:

Einfach langes Format (single format): Formatbreite N = 32 Bit

$\hspace*{2cm} \begin{tabular}{|c|c|c|} \multicolumn{1}{c}{$1$} & \multicolumn{1}{c}{~~~8 Bit~~~} & \multicolumn{1}{c}{~~~~~~23 Bit~~~~~~} \\ \hline $v$ & $e$ & $M$ \\ \hline \end{tabular}\bigskip$

Doppelt langes Format (double format): Formatbreite N = 64 Bit

$\hspace*{2cm} \begin{tabular}{|c|c|c|} \multicolumn{1}{c}{1} & \multicolumn{1}{c}{~~~~11 Bit~~~~} & \multicolumn{1}{c}{~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~52 Bit~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~} \\ \hline $v$ & $e$ & $M$ \\ \hline \end{tabular}\smallskip$

Wie die oben schematisch vorgestellt IEC/IEEE-Codierung in ihren Feinheiten zu verstehen ist, wird in Abschnitt 3.6 erläutert.

Die Mantisse ist eine nicht-negative reelle Zahl in Festpunkt-Codierung

$M = d_1 b^{-1} + d_2 b^{-2} + \cdots + d_p b^{-p}$

bezüglich einer festen Basis b mit dem Binärpunkt (b=2) (Dezimalpunkt (b=10) etc.) genau vor der ersten Ziffer. Es gibt kein Vorzeichen.

Notation:
Position des Binär- bzw. Dezimalpunktes: Die Annahme des (Binär-, Dezimal-) Punktes vor der ersten Stelle der Mantisse M ist willkürlich; ebenso ist die Indizierung mit d₁als erster (engl. most significant) und d_p als letzter (engl. least significant) Stelle - die nicht der Indizierung bei Festpunkt-Zahlensystemen entspricht - bei Gleitpunkt-Zahlensystemen üblich.
Beide Konventionen entsprechen sowohl dem internationalen Norm-Entwurf Language Independent Integer and Floating Point Arithmetik [247] wie auch den Annahmen, die in der ANSI-C- und der Fortran 90 - Norm festgeschrieben sind.

Die dargestellte reelle Zahl x ist gegeben durch

$x = (-1)^v \cdot b^e \cdot M$

wobei v $\in$ {0,1}. Eine solche Zahlenmenge nennt man Gleitpunkt-Zahlensystem F (floating point numbers).
Ein Gleitpunkt-Zahlensystem mit der Basis b, der Mantissenlänge p und dem Exponentenbereich [e_min, e_max] $\subset$ Z enthält die folgenden reellen Zahlen:

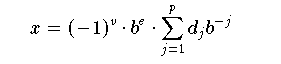
$\begin{equation} \label{eqn:gleitZahlen} x = (-1)^{v}\cdot b^{e} \cdot \sum_{j=1}^{p} d_{j} b^{-j} \end{equation}$
mit

v $\in$ {0,1},
e $\in$ Z, e_min $\leq$ e $\leq$ e_max,
d_j $\in$ {0,1,2,...,b-1}, j = 1,2,....,p;

d_j sind die Ziffern (digits) der Mantisse M = d₁b^-1+d₂b^-2+...+d_pb^-p .

Beispiel:

Zahlendarstellung: Die reelle Zahl 0.1 wird in einem sechsstelligen, dezimalen Gleitpunkt-Zahlensystem (b=10, p=6) als
.100000*10⁰
dargestellt. In einem 24-stelligen, binären Gleitpunkt-Zahlensystem (b=2, p=24) kann 0.1 nicht exakt dargestellt werden; die Näherungsdarstellung
.11001100110011011001101*2^-3
wird stattdessen verwendet.

Größere Mantissenlängen bzw. Exponentenlängen als bei der üblichen "einfachen Genauigkeit" ist möglich. Man spricht oft von "doppelter" bzw. "k-facher" Genauigkeit, obwohl die verwendeten Mantissenlängen p₂, p₃, ... meist keine ganzzahligen Vielfachen der einfachen Mantissenlänge p₁ sind.(doppelte bzw. k-fache Genauigkeit),

Normalisierte und denormalisierte Gleitpunktzahlen:

Es können verschiedene Werte zur gleichen Zahl x führen:
Mehrdeutige Zahlendarstellungen: Die Zahl 0.1 kann in einem dezimalen Gleitpunkt-Zahlensystem mit sechs Mantissenstellen durch

.100000 * 10⁰oder .010000 * 10¹ oder
.001000 * 10²oder .000100 * 10³ oder
.000010 * 10⁴oder .000001 * 10⁵

dargestellt werden. Die Darstellung von 0.1 als Gleitpunktzahlen ist also nicht eindeutig.

Damit die Zahlendarstellung eindeutig wird, kann man zusätzlich die Forderung d₁ $\ne$ 0 stellen. Die so erhaltenen Gleitpunktzahlen mit b^-1 $\leq$ M < 1 heißen normalisierte (oder normale) Gleitpunktzahlen. Für b = 10 ist 0.1 $\leq$ M < 1. Die Menge der normalisierten Gleitpunktzahlen erweitert um die Zahl Null (charakterisiert durch die Mantisse M = 0) wird im folgenden mit F_N bezeichnet.
Durch die Einschränkung d₁ $\ne$ 0 erhält man umkehrbar-eindeutige Beziehungen zwischen den zulässigen Werten

v $\in$ {0,1},
e $\in$ Z, e_min $\leq$ e $\leq$ e_max,
d₁ $\in$ {1,2,...,b-1},
d_j $\in$ {0,1,...,b-1}, j = 2,3,....,p;

und den Zahlen in F_N\{0}.

Tabelle 4.1: Eineindeutige Zuordnung der nichtnegativen Zahlen aus F zu den Tupeln (e,M). Analog für die negativen Zahlen aus F, für die man v = 1 setzt.

Exponent Mantisse

normalisierte Gleitpunktzahlen e $\in$ [e_min, e_max] M $\in$ [b^-1, 1 - b^-p]

denormalisierte Gleitpunktzahlen e = e_min M $\in$ [b^-p, b^-1 - b^-p]

Null e = e_min M = 0

Da wegen d₁ $\ne$ 0 einige Zahlen wegfallen, kann man diese Zahlen zurückgewinnen, indem man d₁ = 0 setzt für e = e_min. Die Zahlen mit M $\in$ [b^-p , b^-1 - b^-p ], die sämtlich im Intervall

$(-b^{e_{\min}-1},b^{e_{\min}-1})$

liegen, heißen denormalisierte (oder subnormale) Zahlen und werden mit F_D bezeichnet. Die Zahl 0 wird zu F_N gezählt.

Parameter eines Gleitpunkt-Zahlensystems:

Jedes Gleitpunkt-Zahlensystem ist durch vier ganzzahlige Parameter und einen Wahrheitswert gekennzeichnet:

1. Basis (base, radix) b $\geq$ 2,

2. Mantissenlänge (precision) p $\geq$ 2,

3. kleinster Exponent e_min < 0,

4. größter Exponent e_max > 0,

5. Normalisierungsindikator denorm $\in$ Boolean;

Der Wahrheitswert denorm gibt an, ob das Gleipunkt-Zahlensystem denormalisierte Zahlen enthält (denorm = true) oder nicht (denorm = false).
Für GZ wird im folgenden die Kurzbezeichnung F(b,p,e_min,e_max,denorm) verwendet. Dabei gilt:

F(b,p,e_min,e_max,true) = F_N(b,p,e_min,e_max) $\cup$ F_D(b,p,e_min,e_max)
F(b,p,e_min,e_max,false) = F_N(b,p,e_min,e_max)

Die Basis b ist heute auf allen Computern 2, 10 oder 16 (binär, dezimal oder hexadezimal).

Beispiele:

Intel:Die Zahlensysteme F(2,24,-125,128,true) und F(2,53,-1021,1024,true) für einfach bzw. doppelt genaue Gleitpunkt-Zahlendarstellung entsprechend der IEC/IEEE-Norm (siehe Abschnitt 3.6) sind die im Normalfall verwendeten Zahlendarstellungen auf Intel-Mikroprozesoren. Darüber hinaus gibt es auch noch das erweitert genaue Gleitpunkt-Zahlensystem F(2,64,-16381,16384,true).
IBM System/390: Die Großrechner (mainframes) der Firma IBM haben drei hexadezimale Gleitpunkt-Zahlensysteme: short precision F(16,6,-64,63,false), long precision F(16,14,-64,63,false) und extended precision F(16,28,-64,63,false).
Taschenrechner: Technisch-naturwissenschaftliche Taschenrechner haben meist nur ein Gleitpunkt-Zahlensystem: das dezimale System F(10,10,-98,100,false). Bei manchen Taschenrechnern ist die Mantissenlänge größer als 10, obwohl am Display maximal 10 Stellen angezeigt werden.

Implizites erstes Bit:

Bei einem GZ kann man bei b = 2 ein Bit zu codieren weglassen, da es im binären nur die Zahlen 0 und 1 gibt, und das 1. Bit ungleich 0 sein muß. D.h., als erste Zahl d₁ muß 1 stehen, d.h. die Mantisse kann ein implizites erstes Bit (engl. hidden bit) besitzen.
Bei subnormalen Zahlen geht das genauso, weil da muß als 1. Ziffer eine 0 stehen.
Vergleiche auch bei den IEC/IEEE-Zahlen das implizite erste Bit.

[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]

	Exponent	Mantisse
normalisierte Gleitpunktzahlen	e $\in$ [e_min, e_max]	M $\in$ [b^-1, 1 - b^-p]
denormalisierte Gleitpunktzahlen	e = e_min	M $\in$ [b^-p, b^-1 - b^-p]
Null	e = e_min	M = 0

1. Basis (base, radix)	b $\geq$ 2,
2. Mantissenlänge (precision)	p $\geq$ 2,
3. kleinster Exponent	e_min < 0,
4. größter Exponent	e_max > 0,
5. Normalisierungsindikator	denorm $\in$ Boolean;