[ < ] [ globale Übersicht ] [Kapitelübersicht ] [ Stichwortsuche ] [ > ]
In sehr vielen Fällen läßt sich die Beantwortung von Fragen, die an ein Modell gestellt werden, zurückführen auf die zahlenmäßige Bestimmung der Werte von Zustandsgrößen (an bestimmten Stellen und zu bestimmten Zeitpunkten). Eine mathematische Aufgabe wird durch Spezifikation von Nebenbedingungen zu einer numerischen Aufgabe: Aus vorgegebenen mathematischen Beziehungen (Gleichungen, Ungleichungen etc.) und numerischen Informationen (Daten) können die zahlenmäßigen Werte der Zustandsgrößen, an denen Interesse besteht, durch rechnerische Verfahren ermittelt werden.
Die numerische Mathematik beschäftigt sich mit dem Entwurf, der Analyse und Implementierung von Verfahren zur computerunterstützten Lösung von numerischen Aufgaben. Weiters stellt die numerische Mathematik mathematische Hilfsmittel zur Verfügung. Obwohl es keine exakte Trennung zwischen numerischer Datenverarbeitung und numerischer Mathematik durchgeführt werden kann (was auch nicht sinnvoll ist), beschäftigt sich die erstere eher mit dem Entwurf, der Implementierung und Bewertung numerischer Software.
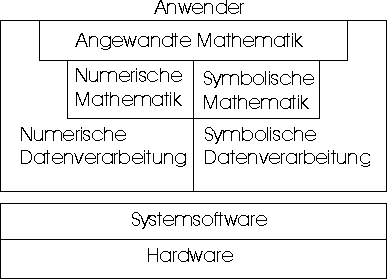
Die folgende Graphik zeigt die zeigt die ungefähre Lage der Numerischen Mathematik und der Numerischen Datenverarbeitung zwischen Anwender und Computer. Man erkennt als Informatiker wohl sofort, daß es unumgänglich ist, sich mit dieser Materie ein wenig auseinanderzusetzen.

Bei der numerischen (nichtsymbolischen) Lösung mathematischer Probleme auf Computern muß man mit den dort verfügbaren Zahlen und Rechenoperationen das Auslangen finden. An Zahlen stehen lediglich endlich viele rationale Zahlen zur Verfügung, die sogenannten Maschinenzahlen (Gleitpunktzahlen). Alle reellen Zahlen, die nicht mit einer derartigen Maschinenzahl übereinstimmen, müssen durch eine der vorhandenen Maschinenzahlen gut approximiert werden. (Wie wir später sehen werden, verursacht diese Näherung natürlich einen Fehler!)
An Rechenoperationen stehen lediglich Näherungen für die arithmetischen Operationen +,-,* und / zur Verfügung; um Näherungen handelt es sich deshalb, weil die Maschinenzahlen bezüglich dieser arithmetischen Operationen nicht abgeschlossen sind: Das exakte Resultat dieser Operationen ist im allgemeinen keine Maschinenzahl und muß durch eine solche approximiert werden.
Genauso ist es mit den elementaren Funktionen sin, cos, exp, log etc. In den meisten Programmiersprachen für numerische Anwendungen gibt es für diese Funktionen vordefinierte Unterprogramme SIN, COS, EXP, LOG etc., d.h. mathematische Software, die als fester Bestandteil in die Programmiersprache einbezogen ist. In diesen Unterprogrammen wird für eine gegebene Argumentwert (eine bestimmte Maschinenzahl) ein Näherungswert berechnet, der im günstigsten Fall aus der dem exakten Funktionswert am nächsten gelegenen Maschinenzahl besteht; er kann unter Umständen aber auch deutlich davon abweichen. Die Verwendung dieser Unterprogramme erfolgt völlig analog zur Verwendung der entsprechenden elementaren Funktionen in der Analysis.
Beispiel:(Pendel): Folgendes C-Programm ist ein Beispiel, wie die iterative Berechnug in einem C-Programm aussehen kann. Es implementiert die Gauß- Methode und liefert Näerungswerte für das vollständige elliptische Integral erster Gattung. Hierbei wird eine Genauigkeit von ca. 7 korrekten Dezimalstellen erzielt.
Der komplette, compilierbare C-Source- Code befindet sich HIER.
Die Operationen der Infinitesimalrechnung sind den numerischen Verfahren prinzipiell verschlossen: Wegen der Endlichkeiten der Menge der Maschinenzahlen gibt es keine beliebig kleinen und beliebig großen Zahlen, auch keine beliebig nahe benachbarten Zahlen. Schon deshalb sind also keine Grenzprozesse möglich. Weiters braucht die Ausführung jeder Rechenoperation Zeit, sodaß Berechnungen auf einem Computer nur aus endlich vielen Rechenschritten bestehen können.
Es ist daher prinzipiell unmöglich, z.B. die Summe einer unendlichen Reihe zu ermitteln; man muß sich mit einer Partialsumme (eine Summe aus endlich vielen Reihengliedern) zufriedengeben. An dieser grundsätzlichen Beschränkung ändern auch superschnelle CPUs und Parallelrechner nichts; die meisten Verfahren der Analysis müssen am Computer durch finite Verfahren ersetzt werden.
Das Abbrechen von unendlichen Reihen, das Ersetzen analytischer Operationen (Differentiation, Integration etc.) durch endlich viele Auswertungen arithmetischer Ausdrücke etc. kann man unter dem Begriff Finitisierung zusammenfassen. Wegen dieser Finitisierung und auf Grund des eingeschränkten Zahlenbereiches, der fehlerbehafteten Arithmetik etc. besteht auf einem Computer meist keine Möglichkeit, das exakte Resultat eines mathematischen Problems zu berechnen; es können nur Näherungswerte für das gesuchte Ergebnis ermittelt werden.
Die Güte eines numerischen Näherungswertes, d.h. die Genauigkeit, mit der er das exakte Ergebnis approximiert, läßt sich oft durch eine Vergrößerung des Rechenaufwandes - mehr Iterationsschritte, aufwendigere Verfahren, feinere Unterteilungen und andere Maßnahmen - steigern; man erreicht jedoch schließlich eine durch die Rechengenauigkeit des Computers oder den erforderlichen Zeitaufwand bedingte Grenze.- Das genaueste Ergebnis bringt nichts, wenn es zu spät verfügbar ist, und das am raschesten zur Verfügung stehende Ergebnis ist sinnlos, wenn es falsch ist. Die numerische Mathematik bietet uns also die Möglichkeit eine Abwägung zwischen Genauigkeit und Geschwindigkeit zu treffen, indem wir den Rechenfehler, den unser Programm verursacht vorherbestimmen können.
Wie man bereits an dem vorigen Beispiel sieht, kann nur in Abhängigkeit vom konkreten Anwendungsfall eine sinnvolle Entscheidung getroffen werden, welchen konkreten Zahlenwert man als „Lösung" akzeptiert. Kann man also die numerische Lösung eines mathematischen Problems nicht vom konkreten Anwendungsproblem trennen?
Da eine derartige Trennung äußerst erstrebenswert ist - sie ermöglicht erst die universelle Anwendbarkeit numerischer Verfahren -, könnte man sich im Falle des Pendels vorstellen, immer einen Näherungswert für die Schwingungsdauer mit der größtmöglichen Anzahl richtiger Stellen numerisch zu ermitteln. Dieser Weg wäre beim Pendelbeispiel gangbar, da in diesem Fall der benötigte Mehraufwand ohne Bedeutung ist.
Ein anderes Bild ergibt sich, wenn man dem Modell des Pendels noch einen Reibungsterm hinzufügt. In diesem Fall muß man konkrete Lösungen der Differentialgleichung im allgemeinen numerisch berechnen und den Abstand der Nullstellen der numerischen Lösung ermitteln. Der Aufwand, der in diesem Fall erforderlich ist, um alle Resultate mit größtmöglicher Genauigkeit zu erhalten, kann nicht mehr vernachlässigt werden. Dieser Situation kann man begegnen, indem man Resultate ermittelt, die einerseits den Genauigkeitsanforderungen des Anwenders entsprechen, aber andererseits einen möglichst geringen Berechnungsaufwand erfordern. Eine in diesem Sinn aufwandsoptimale Lösung besitzt im allgemeinen gerade noch die vom Anwender geforderte Genauigkeit und ist weit von einer Lösung mit maximaler Genauigkeit entfernt.
Hier erkennt man wieder sehr schön, wie wichtig es ist, als Informatiker über derartige Probleme bescheid zu wissen, damit es nicht passiert, daß man ein Programm schreibt, das mit wenigen Daten zwar korrekt und schnell läuft, wenn hingegen mehr Daten benutzt werden, der Rechenaufwand so stark ansteigt, daß der Computer diese Datenflut nicht mehr bewältigen kann, und das alles, obwohl bereits eine einfache Näherung ausgereicht hätte.
[ < ] [ globale übersicht ] [Kapitelübersicht ] [ Stichwortsuche ] [ > ]