[<] [globale Übersicht] [Kapitelübersicht] [Stichwortsuche] [>]

  • 8.11.01 Symmetrische, positiv definite Matrizen:

    Eine spezielle Struktur, die zudem unmittelbar ersichtlich ist, ist die Symmetrie der Koeffizientenmatrix, d.h.

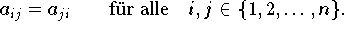
    Unter den symmetrischen Systemen spielen noch diejenigen mit einer positivdefinition Koeffizientenmatrix eine besondere Rolle; sie kommen Z.B. bei der Diskretisierung von Randwertprobleme gewönlicher und partieller differentialgleichungen im zusammenhang mit physikalischen und mechanischen Problemen häufig vor.

    Für positiv definite, symmetrische Matrizen gibt es eine symmetrische Form des Eliminationsalgorthmus zur Berechnung der Cholesky-Zerlgung

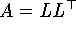
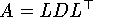
    mit einer unteren Dreiecksmatrix L oder

    mit einer unteren Dreiecksmatrix mit lii=1 und einer positiven Diagonalmatrix D. Man kann bei diesem Algorithmus auf eine Piovtsuche verzichten, ohne daß die Stabilität gefährdet wäre.

    Der Rechenaufwand reduziert sich gegenüber der LU-Zerlegung auf ca.50 %. Auch der Speicherbedarf reduziert sich bei einer Symmetrischenmatrix auf ca. 50%, da die identischen Elemente aij und aji nur ein Mal gespeichert werden müssen. Dies ist unabhängig von einer allfähligen Definitheit der Matrix.

    Wenn A Symmetrisch, aber indefinit ist, gibt es keine Faktorisierung der Form A=LDL . Die Matrix A kann aber in der Form

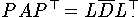
    faktorisiert werden, wobei 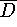eine Blockdiagonalmatrix mit 1x1- und 2x2-Diagonalblöcken ist.

    Auch für indefinite, symmetrische Matrizen gibt es eine besondere algorithmische Form der Dreieckszerlegung, den Bunch-Kaufman-Algorithmus. Dabei kann auf Vertauschungen zur Erhaltung der Stabilität nicht verzichtet werden. Zur Erhaltung der Symmetrie während der Elimination müssen dabei gleuchzeitig entsprechende Zeilen und Spalten vertauscht werden. Die Pivotsuche ist deshalb entlang der Diagonalen vorzunehmen.

    Die Guten stabilitätseigenschaften der Eliminationsalgorithmen für symmetrische, positiv definite Systemme haben nichts mit der Kondition der Koeffizientenmatrizen zu tun. Positiv definite Matrizen können auch sehr schlecht koditioniert sein wie das folgende Beispiel zeigt:

  • Beispiel

    [<] [globale Übersicht] [Kapitelübersicht] [Stichwortliste] [>]