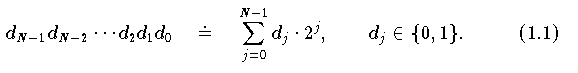
Beispiele:
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]
3.4.1 INTEGER-Zahlensysteme:
Am besten stellt man Integerzahlen in Binärschreibweise der Form: dN-1dN-2...d2d1d0 dar. Diese Zahlen können leicht vom Computer verarbeitet, und auch mit folgender Formel ins Dezimalsystem umgerechnet werden:
0000...0000
0
0000...00011
1111...11112N - 1
Damit werden alle positiven Zahlen von 0 bis 2N - 1 dargestellt. N ist Element der natürlichen Zahlen und gibt die Anzahl der Binärziffern an (d0 bis dN-1). Man
kann auch sagen, es gibt die Anzahl der Bits an, die verwendet werden, um eine Zahl darzustellen.
Man nennt jene Speicherzelle, in der genau eine binäre Ziffer abgespeichert werden kann, ein Bit. Dieser Name leitet sich von "binary digit" ab.
Warum gerade 2N - 1 wird sich vielleicht jemand fragen. Eine Stelle im Binärsystem entspricht ja einem Bit, mit dem man 2 Zahlen darstellen kann, und zwar 0 und
1. Mit 2 Bit kann man 4 (= 22) Zahlen darstellen: 002![]() 010, 012
010, 012![]() 110, 102
110, 102![]() 210 und 112
210 und 112![]() 310. Mit N Bit kann man 2N Zahlen darstellen. Nun kann man sich leicht
ein einfaches Beispiel überlegen:
310. Mit N Bit kann man 2N Zahlen darstellen. Nun kann man sich leicht
ein einfaches Beispiel überlegen:
Angenommen N = 3. Dann ist die kleinste darstellbare Binärzahl gleich 000. Ins Dezimalsystem umgerechnet ergibt das die Zahl 0. Die größte darstellbare
Binärzahl 111 ins Dezimalsystem umgerechent ergibt die Zahl 7, und 7 = 2 * 2 * 2 - 1 = 23 - 1 = 8 - 1. Das sind also 23 = 8 Zahlen, die dargestellt werden können.
Bei 32-Bit-Zahlen können also maximal 232 ![]() 4294967296 (in Worten: über 4Mrd.) Zahlen dargestellt werden.
4294967296 (in Worten: über 4Mrd.) Zahlen dargestellt werden.
Es müssen auch negative Zahlen darstellbar sein. Das geschieht auf 3 Arten: Getrennte Codierung des Vorzeichens, Einerkomplement- und
Zweierkomplementdarstellung. Folgende Variablen werden für die Zahlendarstellungen verwendet: dj, v ![]() {0,1}, j
{0,1}, j ![]() N, v = Vorzeichen.
N, v = Vorzeichen.
Getrennte Codierung des Vorzeichens:
Das Vorzeichen v wird dazu verwendet um zu zeigen, ob die angegebene Binärzahl dN-2...d0 positiv ist, das ist der Fall bei v = 0 oder negativ, bei v = 1.
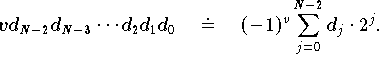
Man erhält damit die ganzen Zahlen [-(2N-1 - 1), 2N-1 - 1] ![]() Z:
Z:
0000...0000 0
1000...0000 -0
0000...0001 1
1000...0001 -1
0111...1111 2N-1 - 1
1111...1111 -(2N-1 - 1)
Wie man sieht, ist die Codierung der Zahl 0 nicht eindeutig (±0). Die größte darstellbare Zahl hat nur mehr den Wert 2N-1 - 1, und die kleinste den Wert -(2N-1 -
1). 2N-1 kommt daher, da die 1.Stelle das Vorzeichen repräsentiert, und daher ein Bit weniger zur Darstellung der eigentlichen Zahl zur Verfügung steht.
Einerkomplement:
Formel zur Darstellung der positiven Zahlen:
Dazu wird die Formel (1.1) verwendet.
Formel zur Darstellung der negativen Zahlen:
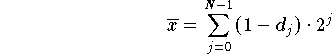
Man erhält wieder die ganzen Zahlen [-(2N-1 - 1), 2N-1 - 1] ![]() Z:
Z:
0000...0000 0
1111...1111 -0
0000...0001 1
1111...1110 -1
0111...1111 2N-1 - 1
1000...0000 -(2N-1 - 1)
Die Codierung der Zahl 0 ist auch hier nicht eindeutig (±0).
Die negativen Zahlen, dargestellt im rechten Teil des obigen Beispiels, unterscheidet sich von den positiven im linken Teil dadurch, daß Nullen und Einser vertauscht
sind. Dieses Komplement erhält man durch (1 - dj), da 1 - 0 = 1 und 1 - 1 = 0 ist. Positive und negative Zahlen können am führenden Bit (dN-1) unterschieden
werden.
Zweierkomplementdarstellung:
Formel zur Darstellung der positiven Zahlen:
Dazu wird wieder die Formel (1.1) verwendet, wie auch beim Einerkomplement.
Formel zur Darstellung der negativen Zahlen:
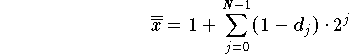
Beispiele:
0000...0000 0
0000...0001 1
1111...1110 -1
0111...1111 2N-1 - 1
1000...0001 -(2N-1 - 1)
1000...0000 -2N-1
Die Codierung der Zahl 0 ist eindeutig, das wird durch das 1 plus der Summe erreicht, allerdings ist jetzt der Zahlenbereich [-2N-1, 2N-1 - 1] unsymmetrisch.
Die Binärzahlen und deren Wert unterscheiden sich beim Einer- und Zweierkomplement um eine Binärziffer bzw. um den Wert 1. Daher kann man auch die
einzelnen Bits mittels des Einerkomplements umwandeln und anschließend 1 addieren.
Eine andere Alternative zur Umrechnung in Zweierkomplement ist, die binären Ziffern von rechts nach links bis zur ersten 1 einschließlich zu kopieren und die
restlichen Ziffern zu komplementieren. Positive und negative Zahlen können wieder am führenden Bit unterschieden werden.
Beispiel:
Intel:Die Intel-Mikroprozessoren haben Zweierkomplement-Codierungen der ganzen Zahlen mit Formatbreiten N = 16, 32 und 64 Bits, die als short integer, word integer und long integer bezeichnet werden. Der Bereich der Word-integer-Zahlen ist [-231,231 - 1] = [-2.147.483.648, 2.147.483.647]
Z.
Datentyp INTEGER:
Integer-Zahlen sind Teilmengen der ganzen Zahlen. Operationen, die auf Integer-Zahlen angewendet werden können sind: +, -, *, div, mod und abs. imin ![]() 0 ist
die kleinste Zahl und imax > 0 ist die größte ganze Zahl. Zum Beispiel imin = 0 entspricht die Menge der nichtnegativen ganzen Zahlen. Bei einer symmetrische
Codierung entspricht imin = -imax, andernfalls spricht man von einer unsymmetrsichen Codierung. Im besonderen gilt imin = -(imax + 1) bei der Codierung
negativer Zahlen durch das Zweierkomplement:
0 ist
die kleinste Zahl und imax > 0 ist die größte ganze Zahl. Zum Beispiel imin = 0 entspricht die Menge der nichtnegativen ganzen Zahlen. Bei einer symmetrische
Codierung entspricht imin = -imax, andernfalls spricht man von einer unsymmetrsichen Codierung. Im besonderen gilt imin = -(imax + 1) bei der Codierung
negativer Zahlen durch das Zweierkomplement:
imin = -2N-1, imax = 2N-1 - 1:
imin = -((2N-1 - 1) + 1) = -2N-1
Beispiel:
C: Auf HP-Workstation-Implementierungen der Programmiersprache C gibt es folgende INTEGER-Zahlensysteme:
| Datentyp | imin | imax |
| unsigned short int | 0 | 65 535 |
| short int | -32 768 | 32 767 |
| unsigned int | 0 | 4 294 967 295 |
| int | -2 147 483 648 | 2 147 483 647 |
| unsigned long int | 0 | 4 294 967 295 |
| long int | -2 147 483 648 | 2 147 483 647 |
Die Datentypen int und long int sind beide mit einer Formatbreite N = 32 Bit codiert. Der Datentyp long int hat somit keine größere Zahlenmenge als der Datentyp int.
Modulo-Arithmetik:
Wenn der Zahlenbereich [imin , imax ] nicht ausreicht (integer overflow), dann kommt entweder eine Fehlermeldung, oder die Zahl wird Modulo gerechnet.
xwrap![]() [imin , imax ],
[imin , imax ],
xwrap![]() x mod m,
x mod m,
m := imax - imin + 1.
Da imin kleiner gleich 0 ist, ist -imin positiv. Der Wert von m ist die Anzahl der Zahlen im Wertebereich [imin, imax]. Die Summe der Absolutbeträge von imin und
imax ergeben nur 2N-1 Zahlen, da die Zahl Null nicht miteingerechnet wurde. Darum muß man am Schluß der Berechnung von m noch 1 dazuzählen.
Beispiele:
Zweierkomplement: imin = -2N-1, imax = 2N-1 - 1
m : = (2N-1-1) - (-2N-1) + 1 = 2*2N-1 (-1+1) = 2*2N-1 = 2N
C: In der im obigen Beispiel behandelten C-Implementierung ist die INTEGER-Arithmetik in allen Fällen eine Module-Arithmetik; eine Umstellung auf
Overflow-Modus ist weder durch Maßnahmen in den C-Programmen noch auf der Ebene des Betriebssystems möglich.
[ < ] [ globale Übersicht ] [ Kapitelübersicht ] [ Stichwortsuche ] [ > ]